题目内容
如图,Rt△AOB的斜边OA在 轴上,且OA =5,OB=4.将Rt△AOB绕原点O逆时针旋转一定的角度,使直角边OB落在
轴上,且OA =5,OB=4.将Rt△AOB绕原点O逆时针旋转一定的角度,使直角边OB落在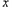 轴的负半轴上得到相应的Rt△A'OB',则A'点的坐标是( )
轴的负半轴上得到相应的Rt△A'OB',则A'点的坐标是( )
 轴上,且OA =5,OB=4.将Rt△AOB绕原点O逆时针旋转一定的角度,使直角边OB落在
轴上,且OA =5,OB=4.将Rt△AOB绕原点O逆时针旋转一定的角度,使直角边OB落在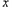 轴的负半轴上得到相应的Rt△A'OB',则A'点的坐标是( )
轴的负半轴上得到相应的Rt△A'OB',则A'点的坐标是( )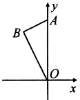
(-4,3)

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
题目内容
 轴上,且OA =5,OB=4.将Rt△AOB绕原点O逆时针旋转一定的角度,使直角边OB落在
轴上,且OA =5,OB=4.将Rt△AOB绕原点O逆时针旋转一定的角度,使直角边OB落在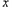 轴的负半轴上得到相应的Rt△A'OB',则A'点的坐标是( )
轴的负半轴上得到相应的Rt△A'OB',则A'点的坐标是( )

 高中必刷题系列答案
高中必刷题系列答案