��Ŀ����
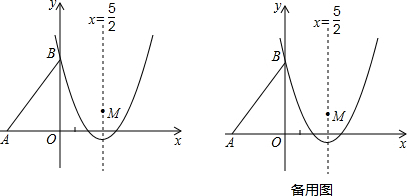
��ͼ��Rt��AOB����ֱ�DZ�OB��OA�ֱ�λ��x�ᡢy���ϣ�OA=6��OB=8��

��1����ͼ1������AOB�۵�����Bǡ�����ڵ�O�����ۺ�ΪCD1�����D1�����ꣻ
��2����ͼ2������AOB�۵�����Oǡ������AB���ϵĵ�C�����ۺ�ΪAD2�����D2�����ꣻ
��3����ͼ3������AOB�۵�����O���ڡ�AOB�ڵĵ�C����OD3=2���ۺ�ΪAD3��AD3��OC���ڵ�E�������C�ĺ����꣮

��1����ͼ1������AOB�۵�����Bǡ�����ڵ�O�����ۺ�ΪCD1�����D1�����ꣻ
��2����ͼ2������AOB�۵�����Oǡ������AB���ϵĵ�C�����ۺ�ΪAD2�����D2�����ꣻ
��3����ͼ3������AOB�۵�����O���ڡ�AOB�ڵĵ�C����OD3=2���ۺ�ΪAD3��AD3��OC���ڵ�E�������C�ĺ����꣮
��������1�������۵������ʿɵ�OD1=BD1��Ȼ�����OD1����д����D1�����꼴�ɣ�
��2�����ù��ɶ�����ʽ���AB���ٸ����۵������ʿɵ�AC=OA��OD2=CD2��Ȼ���ʾ��BC����OD2=x����ʾ��BD2����Rt��BCD2�У����ù��ɶ����г��������x����д����D1�����ꣻ
��3����Rt��AOD3�У����ù��ɶ�����ʽ���AD3�����ݷ��۵����ʿɵ�OE��AD3��OC=2OE��Ȼ�����������ε�������OE�ij����Ӷ��õ�OC�ij�������C��CF��x����F��Ȼ�������AOD3�͡�OFC���ƣ��������������ζ�Ӧ�߳ɱ�����ʽ���OF��CF���ٸ��ݵ�C�ڵ�һ����д�����꼴�ɣ�
��2�����ù��ɶ�����ʽ���AB���ٸ����۵������ʿɵ�AC=OA��OD2=CD2��Ȼ���ʾ��BC����OD2=x����ʾ��BD2����Rt��BCD2�У����ù��ɶ����г��������x����д����D1�����ꣻ
��3����Rt��AOD3�У����ù��ɶ�����ʽ���AD3�����ݷ��۵����ʿɵ�OE��AD3��OC=2OE��Ȼ�����������ε�������OE�ij����Ӷ��õ�OC�ij�������C��CF��x����F��Ȼ�������AOD3�͡�OFC���ƣ��������������ζ�Ӧ�߳ɱ�����ʽ���OF��CF���ٸ��ݵ�C�ڵ�һ����д�����꼴�ɣ�
����⣺��1�����۵������ʵã�OD1=BD1��
���ԣ�OD1=
OB=
��8=4��
���Ե�D1��4��0����
��2����OA=6��OB=8��
��AB=
=
=10��
���۵������ʵã�AC=OA=6��OD2=CD2��
��BC=AB-AC=10-6=4��
��OD2=x����BD2=8-x��
��Rt��BCD2��CD22+BC2=BD22��
��x2+42=��8-x��2��
���x=3��
���D2��������3��0����
��3����Rt��AOD3��AD3=
=
=2
��
�ɷ��۵����ʵã�OE��AD3��OC=2OE��
S��AOD3=
AD3•OE=
OA•OD3��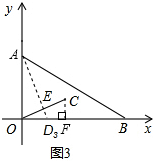
��
��2
OE=
��6��2��
���OE=
��
��OC=2��
=
��
����C��CF��x����F��
�ߡ�COF+��AD3O=180��-90��=90�㣬
��AD3O+��OAD3=90�㣬
���OAD3=��COF��
�֡ߡ�AOD3=��OFC=90�㣬
���AOD3�ס�OFC��
��
=
=
��
��
=
=
=
��
���OF=
��CF=
��
���ԣ���C������Ϊ��
��
����
���ԣ�OD1=
| 1 |
| 2 |
| 1 |
| 2 |
���Ե�D1��4��0����
��2����OA=6��OB=8��
��AB=
| OA2+OB2 |
| 62+82 |
���۵������ʵã�AC=OA=6��OD2=CD2��
��BC=AB-AC=10-6=4��
��OD2=x����BD2=8-x��
��Rt��BCD2��CD22+BC2=BD22��
��x2+42=��8-x��2��
���x=3��
���D2��������3��0����
��3����Rt��AOD3��AD3=
| OA2+OD32 |
| 62+22 |
| 10 |
�ɷ��۵����ʵã�OE��AD3��OC=2OE��
S��AOD3=
| 1 |
| 2 |
| 1 |
| 2 |

��
| 1 |
| 2 |
| 10 |
| 1 |
| 2 |
���OE=
3
| ||
| 5 |
��OC=2��
3
| ||
| 5 |
6
| ||
| 5 |
����C��CF��x����F��
�ߡ�COF+��AD3O=180��-90��=90�㣬
��AD3O+��OAD3=90�㣬
���OAD3=��COF��
�֡ߡ�AOD3=��OFC=90�㣬
���AOD3�ס�OFC��
��
| OF |
| OA |
| CF |
| OD3 |
| OC |
| AD3 |
��
| OF |
| 6 |
| CF |
| 2 |
| ||||
2
|
| 3 |
| 5 |
���OF=
| 18 |
| 5 |
| 6 |
| 5 |
���ԣ���C������Ϊ��
| 18 |
| 5 |
| 6 |
| 5 |
���������⿼���˷��۱任�����ʣ�������ͼ�����ʣ���Ҫ�����˹��ɶ��������������ε��ж������ʣ�������Ŀ����Ǹ����ʲ����ݹ��ɶ����г������ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
 8����ͼ��Rt��AOB��б��OA��y���ϣ���OA=5��OB=4����Rt��AOB��ԭ��O��ʱ����תһ���ĽǶȣ�ʹֱ�DZ�OB����x��ĸ������ϵõ���Ӧ��Rt��A��OB�䣬��A����������
8����ͼ��Rt��AOB��б��OA��y���ϣ���OA=5��OB=4����Rt��AOB��ԭ��O��ʱ����תһ���ĽǶȣ�ʹֱ�DZ�OB����x��ĸ������ϵõ���Ӧ��Rt��A��OB�䣬��A����������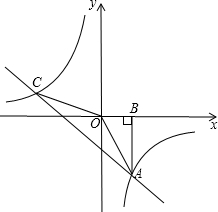 ��ͼ��Rt��AOB�Ķ���A��һ�κ���y=-x+��k+1����ͼ���뷴��������y=
��ͼ��Rt��AOB�Ķ���A��һ�κ���y=-x+��k+1����ͼ���뷴��������y= ��2004•̩������ͼ��Rt��AOB����ֱ�DZ�OA��OB�ij��ֱ���1��3������AOB��O�㰴��ʱ�뷽����ת90�㣬����DOC��λ�ã�
��2004•̩������ͼ��Rt��AOB����ֱ�DZ�OA��OB�ij��ֱ���1��3������AOB��O�㰴��ʱ�뷽����ת90�㣬����DOC��λ�ã�