题目内容
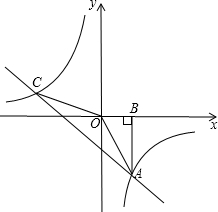 如图,Rt△AOB的顶点A是一次函数y=-x+(k+1)的图象与反比例函数y=
如图,Rt△AOB的顶点A是一次函数y=-x+(k+1)的图象与反比例函数y=| k |
| x |
| 3 |
| 2 |
(1)求这两个函数的解析式;
(2)求出它们的交点A、C的坐标和△AOC的面积.
分析:(1)可设出A的坐标,表示出△AOB的面积,反比例函数的比例系数应等于点A的横纵坐标的积,也就求出一次函数的解析式;
(2)让两个函数解析式组成方程组求出A、C的坐标,设直线与y轴的交点是D,把△AOC分割为△BCD和△AOD的面积的和.
(2)让两个函数解析式组成方程组求出A、C的坐标,设直线与y轴的交点是D,把△AOC分割为△BCD和△AOD的面积的和.
解答: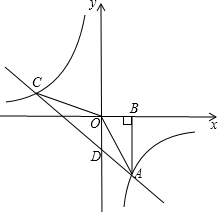 解:(1)设点A坐标为(m,n),则OB=m,AB=-n.
解:(1)设点A坐标为(m,n),则OB=m,AB=-n.
∵A(m,n)在反比例函数y=
的图象上,
∴n=
,即k=mn.
∵S△AOB=
•OB•AB=
•m•(-n)=
,
∴k=mn=-3(3分),
∴反比例函数的解析式是y=
,一次函数的解析式是y=-x-2.(5分);
(2)根据题意得
解得x=1,y=-3或x=-3,y=1
∴A(1,-3)、C(-3,1)(7分),
设直线与y轴的交点是D,
∴S△AOC=
×2×1+
×2×3=4.(10分).
 解:(1)设点A坐标为(m,n),则OB=m,AB=-n.
解:(1)设点A坐标为(m,n),则OB=m,AB=-n.∵A(m,n)在反比例函数y=
| k |
| x |
∴n=
| k |
| m |
∵S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴k=mn=-3(3分),
∴反比例函数的解析式是y=
| -3 |
| x |
(2)根据题意得
|
∴A(1,-3)、C(-3,1)(7分),
设直线与y轴的交点是D,
∴S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:过某个点,这个点的坐标应适合这个函数解析式.在坐标轴上的三角形的面积通常选用被y轴分割成的两个三角形的面积的和.

练习册系列答案
相关题目
 8、如图,Rt△AOB的斜边OA在y轴上,且OA=5,OB=4.将Rt△AOB绕原点O逆时针旋转一定的角度,使直角边OB落在x轴的负半轴上得到相应的Rt△A′OB′,则A′点的坐标是
8、如图,Rt△AOB的斜边OA在y轴上,且OA=5,OB=4.将Rt△AOB绕原点O逆时针旋转一定的角度,使直角边OB落在x轴的负半轴上得到相应的Rt△A′OB′,则A′点的坐标是
 (2004•泰安)如图,Rt△AOB的两直角边OA、OB的长分别是1和3,将△AOB绕O点按逆时针方向旋转90°,至△DOC的位置.
(2004•泰安)如图,Rt△AOB的两直角边OA、OB的长分别是1和3,将△AOB绕O点按逆时针方向旋转90°,至△DOC的位置.