题目内容
【题目】如图,△ABC中,AB=AC,F为BC的中点,D为CA延长线上一点,∠DFE=∠B.
(1)求证:△CDF∽△BFE;
(2)若EF∥CD,求证:2CF2=ACCD.

【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据外角的性质得到∠EFB=∠FDC,由等腰三角形的性质得到∠C=∠B,证得△CDF∽△BFE;
(2)根据平行线的性质得到∠EFD=∠FDC,∠C=∠EFB,根据等腰三角形的性质得到∠B=∠C,等量代换得到∠FDC=∠C,推出△CDF∽△BCA,根据相似三角形的性质得到结论.
(1)证明:∵∠DFB=∠DFE+∠EFB=∠C+∠FDC,
∴∠EFB=∠FDC,
∵AB=AC,
∴∠C=∠B,
∴△CDF∽△BFE;
(2)∵EF∥CD,
∴∠EFD=∠FDC,
∵∠B=∠C,∠DEG=∠B,
∴∠FDC=∠C=∠B,
∴△CDF∽△BCA,
∴![]() ,
,
∵BC=2CF,DF=CF,
∴![]() ,
,
∴2CF2=ACCD.

【题目】一个金属棒在不同温度下,其长度也不同,其变化情况如下表:
温度/℃ | … | -5 | 0 | 5 | 10 | 15 | … |
长度/ | … | 13.9 | 13.95 | 14 | 14.05 | 14.1 | … |
(1)上述两个变量中,自变量是 ;
(2)设自变量为![]() ,因变量为
,因变量为![]() ,求出
,求出![]() 关于
关于![]() 的解析式;
的解析式;
(3)当温度为30℃时,求金属棒的长度;
(4)若某天金属棒的长度是14.18![]() ,则当天的气温约是多少℃?
,则当天的气温约是多少℃?
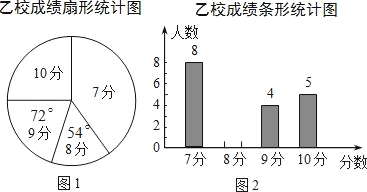
【题目】(10分)甲、乙两校参加市教育局举办的初中生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表.
分数 | 7分 | 8分 | 9分 | 10分 |
人数 | 11 | 0 |
| 8 |
(1)请将甲校成绩统计表和图2的统计图补充完整;
(2)经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好.
【题目】二次函数![]() (a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
(a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
给出了结论:
(1)二次函数![]() 有最小值,最小值为﹣3;
有最小值,最小值为﹣3;
(2)当![]() 时,y<0;
时,y<0;
(3)二次函数![]() 的图象与x轴有两个交点,且它们分别在y轴两侧.
的图象与x轴有两个交点,且它们分别在y轴两侧.
则其中正确结论的个数是
A. 3 B. 2 C. 1 D. 0