Question

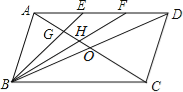
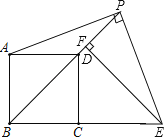
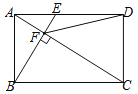
【题目】如图，在矩形ABCD中，E是AD边的中点，BE⊥AC于点F，连接DF，给出下列四个结论：①△AEF∽△CAB；②CF＝2AF；③DF＝DC；④S△ABF：S四边形CDEF＝2：5，其中正确的结论有（ ）

A. 1个B. 2个C. 3个D. 4个

Answer 1

【答案】D

【解析】

①根据四边形ABCD是矩形，BE⊥AC，可得∠ABC=∠AFB=90°，又∠BAF=∠CAB，于是△AEF∽△CAB，故①正确；
②根据点E是AD边的中点，以及AD∥BC，得出△AEF∽△CBF，根据相似三角形对应边成比例，可得CF=2AF，故②正确；
③过D作DM∥BE交AC于N，得到四边形BMDE是平行四边形，求出BM=DE=

BC，得到CN=NF，根据线段的垂直平分线的性质可得结论，故③正确；
④根据△AEF∽△CBF得到EF与BF的比值，以及AF与AC的比值，据此求出S△AEF=S△ABF，S△ABF=S矩形ABCD，可得S四边形CDEF=S△ACD-S△AEF=S矩形ABCD，即可得到S四边形CDEF=S△ABF，故④正确．

如图，过D作DM∥BE交AC于N，

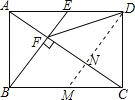
∵四边形ABCD是矩形，

∴AD∥BC，∠ABC＝90°，AD＝BC，

∵BE⊥AC于点F，

∴∠EAC＝∠ACB，∠ABC＝∠AFE＝90°，

∴△AEF∽△CAB，故①正确；

∵AD∥BC，

∴△AEF∽△CBF，∴＝，

∵AE＝AD＝BC，

∴＝，∴CF＝2AF，故②正确，

∵DE∥BM，BE∥DM，

∴四边形BMDE是平行四边形，

∴BM＝DE＝BC，∴BM＝CM，

∴CN＝NF，

∵BE⊥AC于点F，DM∥BE，

∴DN⊥CF，∴DF＝DC，故③正确；

∵△AEF∽△CBF，

∴＝＝，

∴S△AEF＝S△ABF，S△ABF＝S矩形ABCD，

∴S△AEF＝S矩形ABCD，

又∵S四边形CDEF＝S△ACD﹣S△AEF＝S矩形ABCD﹣S矩形ABCD＝S矩形ABCD，

∴S△ABF：S四边形CDEF＝2：5，故④正确；

故选：D．