题目内容
【题目】在下面的网格中,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,已知B,C两点的坐标分别为(﹣3,0),(﹣1,﹣1).
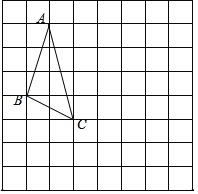
(1)请在图中画出平面直角坐标系,并直接写出点A的坐标.
(2)将△ABC绕着坐标原点顺时针旋转90°,画出旋转后的△A′B'C′.
(3)接写出在上述旋转过程中,点A所经过的路径长.
【答案】(1)见解析,A点坐标为(﹣2,3);(2)见解析;(3)点A所经过的路径长=![]() .
.
【解析】
(1)利用B、C点的坐标建立直角坐标系,然后写出A点坐标;
(2)利用网格特点和旋转的性质画出A、B、C的对应点A′、B′、C′,从而得到△A′B'C′;
(3)先利用勾股定理计算出OA,然后利用弧长公式计算点A所经过的路径长.
解:(1)如图,A点坐标为(﹣2,3);
(2)如图,△A′B′C′为所作;
(2)如图,OA=![]() ,
,
所以点A所经过的路径长=![]() ,
,
△A2B2C2为所作;点A2的坐标为(﹣1,﹣1).
 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目