题目内容
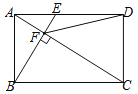
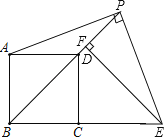
【题目】如图,点P是正方形ABCD的对角线BD延长线上的一点,连接PA,过点P作PE⊥PA交BC的延长线于点E,过点E作EF⊥BP于点F,则下列结论中:①PA=PE;②CE=![]() PD;③BF﹣PD=
PD;③BF﹣PD=![]() BD;④S△PEF=S△ADP,正确的是___(填写所有正确结论的序号)
BD;④S△PEF=S△ADP,正确的是___(填写所有正确结论的序号)
【答案】①②③.
【解析】
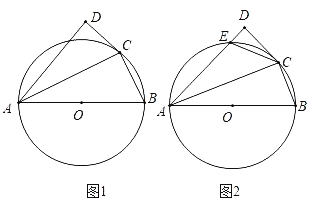
①解法一:如图1,作辅助线,构建三角形全等和平行四边形,证明![]() ,得BG=PE,再证明四边形ABGP是平行四边形,可得结论;
,得BG=PE,再证明四边形ABGP是平行四边形,可得结论;
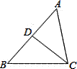
解法二:如图2,连接AE,利用四点共圆证明△APE是等腰直角三角形,可得结论;
②如图3,作辅助线,证明四边形DCGP是平行四边形,可得结论;
③证明四边形OCGF是矩形,可作判断;
④证明![]() ,则
,则![]() ,可作判断.
,可作判断.
①解法一:如图1,在EF上取一点G,使FG=FP,连接BG、PG,
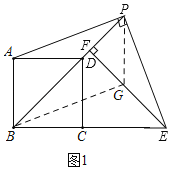
∵EF⊥BP,
∴∠BFE=90°,
∵四边形ABCD是正方形,
∴∠FBC=∠ABD=45°,
∴BF=EF,
在△BFG和△EFP中,
∵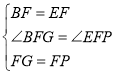 ,
,
∴△BFG≌△EFP(SAS),
∴BG=PE,∠PEF=∠GBF,
∵∠ABD=∠FPG=45°,
∴AB∥PG,
∵AP⊥PE,
∴∠APE=∠APF+∠FPE=∠FPE+∠PEF=90°,
∴∠APF=∠PEF=∠GBF,
∴AP∥BG,
∴四边形ABGP是平行四边形,
∴AP=BG,
∴AP=PE;
解法二:如图2,连接AE,∵∠ABC=∠APE=90°,
∴A、B、E、P四点共圆,
∴∠EAP=∠PBC=45°,
∵AP⊥PE,
∴∠APE=90°,
∴△APE是等腰直角三角形,
∴AP=PE,
故①正确;
②如图3,连接CG,由①知:PG∥AB,PG=AB,
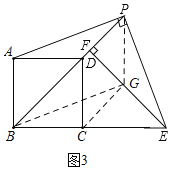
∵AB=CD,AB∥CD,
∴PG∥CD,PG=CD,
∴四边形DCGP是平行四边形,
∴CG=PD,CG∥PD,
∵PD⊥EF,
∴CG⊥EF,即∠CGE=90°,
∵∠CEG=45°,
∴![]() ;
;
故②正确;
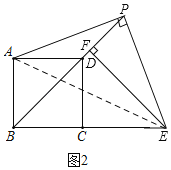
③如图4,连接AC交BD于O,由②知:∠CGF=∠GFD=90°,
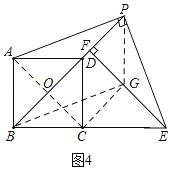
∵四边形ABCD是正方形,
∴AC⊥BD,
∴∠COF=90°,
∴四边形OCGF是矩形,
∴CG=OF=PD,
∴![]() ,
,
故③正确;
④如图4中,在△AOP和△PFE中,
∵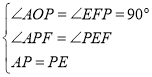 ,
,
∴△AOP≌△PFE(AAS),
∴![]() ,
,
∴![]() ,
,
故④不正确;
本题结论正确的有:①②③,
故答案为:①②③.