题目内容
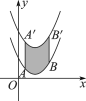
【题目】如图,将函数y=![]() (x-2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A′,B′,若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是__________.
(x-2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A′,B′,若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是__________.
【答案】y=![]() (x-2)2+4
(x-2)2+4
【解析】
先根据二次函数图象上点的坐标特征求出A、B两点的坐标,再过A作AC∥x轴,交B′B的延长线于点C,则C(4,1![]() ),AC=4-1=3,根据平移的性质以及曲线段AB扫过的面积为9(图中的阴影部分),得出AA′=3,然后根据平移规律即可求解.
),AC=4-1=3,根据平移的性质以及曲线段AB扫过的面积为9(图中的阴影部分),得出AA′=3,然后根据平移规律即可求解.
∵函数y=![]() (x-2)2+1的图象过点A(1,m),B(4,n),
(x-2)2+1的图象过点A(1,m),B(4,n),
∴m=![]() (1-2)2+1=1
(1-2)2+1=1![]() ,n=
,n=![]() (4-2)2+1=3,
(4-2)2+1=3,
∴A(1,1![]() ),B(4,3),
),B(4,3),
过A作AC∥x轴,交B′B的延长线于点C,则C(4,1![]() ),
),
∴AC=4-1=3,
∵曲线段AB扫过的面积为9(图中的阴影部分),
∴ACAA′=3AA′=9,
∴AA′=3,
即将函数y=![]() (x-2)2+1的图象沿y轴向上平移3个单位长度得到一条新函数的图象,
(x-2)2+1的图象沿y轴向上平移3个单位长度得到一条新函数的图象,
∴新图象的函数表达式是y=![]() (x-2)2+4.
(x-2)2+4.
故答案是:y=![]() (x-2)2+4.
(x-2)2+4.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目