题目内容
【题目】如图,已知△ABC,AB=AC,将△ABC沿边BC翻折,得到的△DBC与原△ABC拼成四边形ABDC.求证:四边形ABDC是菱形.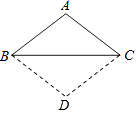
【答案】解:由翻转变换的性质可知,BA=BD,CA=CD,
∵AB=AC,
∴AB=BD=DC=CA,
∴四边形ABDC是菱形
【解析】由翻转变换的性质可知,BA=BD,CA=CD,由AB=AC,得到AB=BD=DC=CA,所以四边形ABDC是菱形.
【考点精析】本题主要考查了等腰三角形的性质和菱形的判定方法的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形才能正确解答此题.

练习册系列答案
相关题目