��Ŀ����
����Ŀ���������⣬����������⣺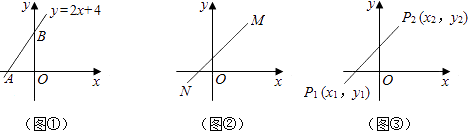
��1����ͼ�٣���ֱ֪��y=2x+4��x�ᡢy��ֱ���A��B���㣬���߶�AB�ij���
��2����ͼ�ڣ���ȣ�1���������̣�����ͨ������ֱ�������εķ������������M��3��4����N����2����1��֮��ľ��룻
��3����ͼ�ۣ�P1��x1 �� y1����P2��x2 �� y2����ƽ��ֱ������ϵ�ڵ����㣬��������ͼ�۹���ֱ�������Σ���ֱ��д��P1P2�ij��ȣ��ú���x1 �� x2 �� y1 �� y2�Ĵ���ʽ��ʾ����
���𰸡�
��1���⣺��ͼ�٣���y=0�ã�2x+4=0��
x=��2��
��A����2��0����
��OA=2��
��x=0ʱ��y=4��
��B��0��4����
��OB=4��
��Rt��AOB�У��ɹ��ɶ����ã�AB= ![]() =2
=2 ![]()
��2���⣺��ͼ�ڣ���M��MP��x�ᣬ��N��NP��y�ᣬMP��NP����P����MP��NP��
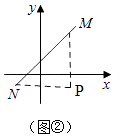
��M��3��4����N����2����1����
��P��3����1����
��MP=4������1��=5��NP=3������2��=5��
��Rt��MNP�У��ɹ��ɶ����ã�MN= ![]() =5
=5 ![]()
��3���⣺��ͼ�ۣ���P2��P2P��x�ᣬ��P1��P1P��y�ᣬP1P��P2P����P����P1P��P2P��
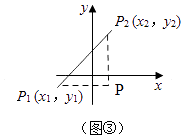
��P1��x1��y1����P2��x2��y2����
��P��x1��y1����
��P1P=x2��x1��P2P=y2��y1��
��Rt��P1P2P�У��ɹ��ɶ����ã�P1P2= ![]() ��
��
����������1����ͼ�٣���y=0�ã�2x+4=0���õ�x=��2��A����2��0�����õ�OA=2����x=0ʱ��y=4���õ�B��0��4����OB=4����Rt��AOB�У��ɹ��ɶ����ã�AB=![]() =2
=2![]() ����2����ͼ�ڣ���M��MP��x�ᣬ��N��NP��y�ᣬMP��NP����P����MP��NP���õ�M��3��4����N����2����1����P��3����1������MP=4������1��=5��NP=3������2��=5����Rt��MNP�У��ɹ��ɶ����ã�MN=
����2����ͼ�ڣ���M��MP��x�ᣬ��N��NP��y�ᣬMP��NP����P����MP��NP���õ�M��3��4����N����2����1����P��3����1������MP=4������1��=5��NP=3������2��=5����Rt��MNP�У��ɹ��ɶ����ã�MN=![]() =5
=5![]() ����3����ͼ�ۣ���P2��P2P��x�ᣬ��P1��P1P��y�ᣬP1P��P2P����P����P1P��P2P����ΪP1��x1��y1����P2��x2��y2�����õ�P��x1��y1��������P1P=x2��x1��P2P=y2��y1����Rt��P1P2P�У��ɹ��ɶ����ã�P1P22=��x2-x1 ��2+��y2-y1��2.
����3����ͼ�ۣ���P2��P2P��x�ᣬ��P1��P1P��y�ᣬP1P��P2P����P����P1P��P2P����ΪP1��x1��y1����P2��x2��y2�����õ�P��x1��y1��������P1P=x2��x1��P2P=y2��y1����Rt��P1P2P�У��ɹ��ɶ����ã�P1P22=��x2-x1 ��2+��y2-y1��2.
�����㾫����������Ĺؼ���������һ�κ��������ʵ����֪ʶ������һ��أ�һ�κ���y=kx+b���������ʣ���1����k>0ʱ��y��x�����������2����k<0ʱ��y��x���������С��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�