Question

【题目】综合题
（1）感知：如图①，四边形ABCD、CEFG均为正方形．易知BE=DG．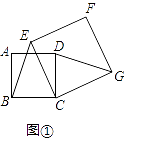

（2）探究：如图②，四边形ABCD、CEFG均为菱形，且∠A=∠F．求证：BE=DG．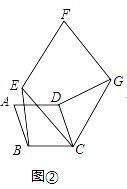

（3）如图③，四边形ABCD、CEFG均为菱形，点E在边AD上，点G在AD的延长线上．若AE=3ED，∠A=∠F，△EBC的面积为8，则菱形CEFG的面积为 ．

Answer 1

【答案】
（1）证明：∵四边形ABCD、四边形CEFG均为正方形，

∴BC=CD，CE=CG，∠BCD=∠ECG=90°，

∴∠BCD﹣∠ECD=∠ECG﹣∠ECD，

即∠BCE=∠DCG，

在△BCE和△DCG中，

，

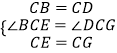∴△BCE≌△DCG，

∴BE=DG．

（2）∵四边形ABCD、四边形CEFG均为菱形，

∴BC=CD，CE=CG，∠BCD=∠A，∠ECG=∠F，

∵∠A=∠F，

∴∠BCD=∠ECG，

∴∠BCD﹣∠ECD=∠ECG﹣∠ECD，

即∠BCE=∠DCG，

∴△BCE≌△DCG．，

∴BE=DG．

（3）20
【解析】解：

应用：∵四边形ABCD是菱形，S△EBC=8，

∴S△AEB+S△EDC=8，

∵AE=3DE，

∴S△AEB=3S△EDC，

∴S△EDC=6，S△EDC=2，

∵△BCE≌△DCG，

∴S△DGC=S△EBC=8，

∴S△ECG=8+2=10，

∴菱形CEFG的面积=2S△EGC=20，

所以答案是20．

【考点精析】掌握正方形的性质是解答本题的根本，需要知道正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．