题目内容
【题目】如图所示,四边形![]() 和
和![]() 分别是边长为
分别是边长为![]() 和
和![]() 的正方形.
的正方形.

(1)用含![]() 和
和![]() 的代数式表示图中三角形
的代数式表示图中三角形![]() 的面积.
的面积.
(2)用用![]() 和
和![]() 的代数式表示图中阴影部分的面积.
的代数式表示图中阴影部分的面积.
(3)小军计算出当![]() ,
,![]() 时的阴影部分面积,与小明计算的当
时的阴影部分面积,与小明计算的当![]() ,
,![]() 时的阴影部分面积相等,为什么呢?请说明理由,并求出此时的阴影部分面积.
时的阴影部分面积相等,为什么呢?请说明理由,并求出此时的阴影部分面积.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)理由见解析;50.
;(3)理由见解析;50.
【解析】
(1)直接根据三角形的面积公式求解即可‘
(2)连接DF,图中阴影部分的面积为![]() ,即可得解;
,即可得解;
(3)阴影部分的面积只与y有关,小军与小明计算的y相等,故阴影部分面积相等;将y代入阴影部分面积公式中即可得解.
(1)由已知得,
![]()
(2)连接DF,如图所示:
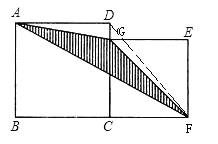
AD=DC=x,CG =CF=y
DG=DC-CG=x-y
![]()
=![]()
=![]()
=![]()
=![]()
(3)由(2)中,得
阴影部分的面积只与y有关,小军与小明计算的y相等,故阴影部分面积相等;
![]()

练习册系列答案
相关题目
【题目】一病人发高烧进医院进行治疗,医生给他开了药并挂了水,同时护士每隔1小时对病人测体温,及时了解病人的好转情况,现护士对病人测体温的变化数据如下表:
时 间 | 7:00 | 8:00 | 9:00 | 10:00 | 11:00 | 12:00 | 13:00 | 14:00 | 15:00 |
体温 | 升0.2 | 降1.0 | 降0.8 | 降1.0 | 降0.6 | 升0.4 | 降0.2 | 降0.2 | 降0 |
注:病人早晨进院时医生测得病人体温是40.2℃。
问:(1)病人什么时候体温达到最高,最高体温是多少?
(2)病人中午12点时体温多高?
(3)病人几点后体温稳定正常?(正常体温是37℃)