题目内容
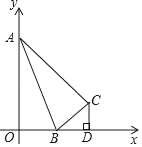
【题目】(1)如图,已知,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,求AB与CD的长.

(2)如图,用3个全等的菱形构成活动衣帽架,顶点A、E、F、C、G、H是上、下两排挂钩,根据需要可以改变挂钩之间的距离(比如AC两点可以自由上下活动),若菱形的边长为13厘米,要使两排挂钩之间的距离为24厘米,并在点B、M处固定,则B、M之间的距离是多少?

【答案】(1)AB=10,CD=4.8;(2)BM=30厘米.
【解析】
(1)在直角三角形ABC中,利用勾股定理求出AB的长,再利用面积法求出CD的长即可.
(2)连接AC,BD交于点O,根据四边形ABCD是菱形求出AO的长,然后根据勾股定理求出BO的长,于是可以求出B、M两点的距离.
解:(1)在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,
由勾股定理得:AB= ![]() =10,
=10,
∵S△ABC= ![]() ABCD=
ABCD= ![]() ACBC,∴CD=
ACBC,∴CD= ![]() =
=![]() =4.8
=4.8
(2).连接AC,BD交于点O,
∵四边形ABCD是菱形,
∴AO= ![]() AC=12厘米,AC⊥BD,
AC=12厘米,AC⊥BD,
∴BO= ![]() =
= ![]() =5厘米,
=5厘米,
∴BD=2BO=10厘米,
∴BM=3BD=30厘米.
故答案为:(1)AB=10,CD=4.8;(2)BM=30厘米.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目