题目内容
【题目】在△ABC中,点D是AB边上一点(不与AB重合),AD=kBD,过点D作∠EDF+∠C=180°,与CA、CB分别交于E、F.
(1)如图1,当DE=DF时,求![]() 的值.
的值.
(2)如图2,若∠ACB=90°,∠B=30°,DE=m,求DF的长(用含k,m的式子表示)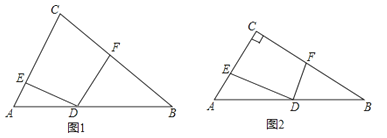
【答案】解:(1)如图1,连接CD,
∵∠EDF+∠C=180°,
∴D,E,C,F四点共圆,
∵DE=DF,
∴∠DCE=∠DCF,
根据正弦定理得![]() ①,
①,![]() ,
,
∴![]() ,②,
,②,
∵∠ADC=180°﹣∠BDC,
∴sin∠ADC=sin∠BDC,
①÷②d得,![]() ,
,
∵AD=kBD,
∴![]() =k;
=k;
(2)∵∠ACB=90°,∠B=30°,
∴∠A=60°,
根据正弦定理得:![]() ③,
③,![]() ,④,
,④,
由(1)知D,E,C,F四点共圆,
∴∠DEA+∠DFB=180°,
∴sin∠DEA=sin∠DFB,④÷③得:![]() ,
,
∴DF=![]() ,
,
∵AD=kBD,DE=m,
∴DF=![]() .
.
【解析】(1)连接CD,由∠EDF+∠C=180°,推出D,E,C,F四点共圆,根据正弦定理得![]() ①,
①,![]() , ②,①÷②得,
, ②,①÷②得,![]() , 根据AD=kBD,根据得到结论;
, 根据AD=kBD,根据得到结论;
(2)根据三角形的内角和得到∠A=60°,根据正弦定理得:![]() ③,
③,![]() , ④,④÷③得:
, ④,④÷③得:![]() , 求得DF=
, 求得DF=![]() , 即可得到结论.
, 即可得到结论.
【考点精析】根据题目的已知条件,利用相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
相关题目



