题目内容
【题目】如图,抛物线经过![]() ,
, ![]() ,
, ![]() 三点.
三点.
(![]() )求出抛物线的解析式.
)求出抛物线的解析式.
(![]() )
)![]() 是抛物线上一动点,过
是抛物线上一动点,过![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,是否存在
,是否存在![]() 点,使得以
点,使得以![]() ,
, ![]() ,
, ![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请求出符合条件的点
相似?若存在,请求出符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

【答案】(![]() )
)![]() (
(![]() )
)![]() 点的坐标为
点的坐标为![]() 或
或![]() 或
或![]() .
.
【解析】试题分析:(1)根据已知条件,设该抛物线的解析式为![]() ,再把点C(0,-2)代入,即可得到结果;
,再把点C(0,-2)代入,即可得到结果;
(2)先设P(m,n),从而得出PM,AM,OA,OC,再分两种情况进行讨论:①当![]() 时,②当
时,②当![]() 时,分别求出点P的坐标即可.
时,分别求出点P的坐标即可.
试题解析:解:(![]() )设抛物线解析式为
)设抛物线解析式为![]() ,将
,将![]() 代入,得:
代入,得: ![]() ,
,
解得![]() ,∴
,∴![]() .
.
(![]() )设
)设![]() 点坐标为
点坐标为![]() ,则
,则![]() .
.
∵![]() 轴于
轴于![]() ,∴
,∴![]() ,
, ![]() ,
, ![]() .
.
∵![]() ,
, ![]() ,∴
,∴![]() ,
, ![]() .
.
分两种情况讨论:
①若![]() ,则
,则![]() ,∴
,∴![]() ,即
,即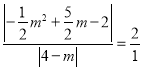 ,解得:
,解得: ![]() 或
或![]() ,∴
,∴![]() ,
, ![]() ;
;
②若![]() ,则
,则![]() ,∴
,∴![]() ,即
,即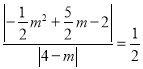 ,解得:
,解得: ![]() (舍)或
(舍)或![]() ,∴
,∴![]() .
.
综上所述: ![]() 点的坐标为
点的坐标为![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
【题目】争创全国文明城市,从我做起,某学校在七年级开设了文明礼仪校本课程,为了解学生的学习情况,学校随机抽取30名学生进行测试,成绩如下(单位:分):78 83 86 86 90 94 97 92 89 86 84 81 81 84 86 88 92 89 86 83 81 81 85 86 89 93 93 89 85 93,整理上面的数据得到频数分布表和频数分布直方图:
成绩(分) | 频数 |
| 5 |
|
|
| 11 |
|
|
| 2 |
回答下列问题:
(1)以上30个数据中,中位数是_____;频数分布表中![]() ____;
____;![]() _____;
_____;
(2)补全频数分布直方图;
(3)若成绩不低于86分为优秀,估计该校七年级300名学生中,达到优秀等级的人数.





