题目内容
【题目】某校九年级两个班，各选派10名学生参加学校举行的“汉字听写”大赛预赛．各参赛选手的成绩如图：
九（1）班：88，91，92，93，93，93，94，98，98，100
九（2）班：89，93，93，93，95，96，96，98，98，99
通过整理，得到数据分析表如下：
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
九（1）班 | 100 | m | 93 | 93 | 12 |
九（2）班 | 99 | 95 | n | 93 | 8．4 |
（1）直接写出表中m、n的值；
（2）依据数据分析表，有人说：“最高分在（1）班，（1）班的成绩比（2）班好”，但也有人说（2）班的成绩要好，请给出两条支持九（2）班成绩好的理由；
（3）若从两班的参赛选手中选四名同学参加决赛，其中两个班的第一名直接进入决赛，另外两个名额在四个“98分”的学生中任选二个，试求另外两个决赛名额落在同一个班的概率．
【答案】（1）94；95．5；（2）略；（3）
．
【解析】试题（1）求出九（1）班的平均分确定出m的值，求出九（2）班的中位数确定出n的值即可；
（2）分别从平均分，方差，以及中位数方面考虑，写出支持九（2）班成绩好的原因；
（3）画树状图得出所有等可能的情况数，找出另外两个决赛名额落在同一个班的情况数，即可求出所求的概率．
试题解析：解：（1）m=
（88+91+92+93+93+93+94+98+98+100）=94；
把九（2）班成绩排列为：89，93，93，93，95，96，96，98，98，99，
则中位数n=
（95+96）=95．5；
（2）①九（2）班平均分高于九（1）班；②九（2）班的成绩比九（1）班稳定；③九（2）班的成绩集中在中上游，故支持九（2）班成绩好（任意选两个即可）；
（3）用A1，B1表示九（1）班两名98分的同学，C2，D2表示九（2）班两名98分的同学，
画树状图，如图所示：
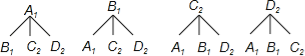
所有等可能的情况有12种，其中另外两个决赛名额落在同一个班的情况有4种，
则P（另外两个决赛名额落在同一个班）=
=．
