题目内容
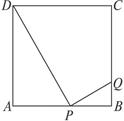
如图,正方形ABCD边长是16 cm,P是AB上任意一点(与A、B不重合),QP⊥DP.设AP="x" cm,BQ="y" cm.试求出y与x之间的函数关系式.

y=-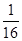 x2+x
x2+x
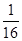 x2+x
x2+x∵ABCD是正方形,
∴∠A=∠B=90°,
∠ADP+∠APD=90°.
又∵QP⊥DP,∴∠APD+∠QPB=90°.
∴∠ADP=∠QPB.
∴有△ADP∽△BPQ.
∴ =
=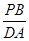 .
.
∴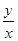 =
=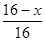 .∴y=-
.∴y=-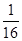 x2+x.
x2+x.
∴∠A=∠B=90°,
∠ADP+∠APD=90°.
又∵QP⊥DP,∴∠APD+∠QPB=90°.
∴∠ADP=∠QPB.
∴有△ADP∽△BPQ.
∴
 =
=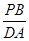 .
.∴
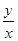 =
=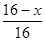 .∴y=-
.∴y=-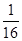 x2+x.
x2+x.
练习册系列答案
相关题目
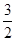 ),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.
),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.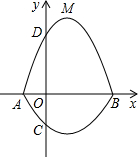
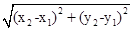 .
.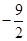 );Rt△ABC的直角边BC在x轴上,直角顶点C的坐标为(
);Rt△ABC的直角边BC在x轴上,直角顶点C的坐标为( ,0),且BC=5,AC=3(如图1).
,0),且BC=5,AC=3(如图1).
 关于x轴对称的抛物线的解析式是 .
关于x轴对称的抛物线的解析式是 . 向左平移2个单位,再向上平移2个单位,得到的抛物线解析式为
向左平移2个单位,再向上平移2个单位,得到的抛物线解析式为

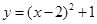

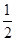 x2-7x+
x2-7x+ ,若自变量x分别取x1,x2,x3,且0<x1<x2<x3,则对应的函数值y1,y2,y3的大小关系正确的是( )
,若自变量x分别取x1,x2,x3,且0<x1<x2<x3,则对应的函数值y1,y2,y3的大小关系正确的是( )