题目内容
【题目】操作实践
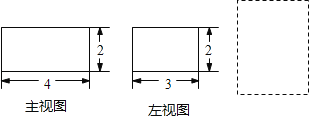
(1)操作1:将矩形ABCD沿对角线AC折叠(如图1),猜想重叠部分是什么图形?并验证你的猜想.连结BE与AC有什么位置关系?
(2)操作2:折叠矩形ABCD,让点B落在对角线AC上(如图2),若AD=4,AB=3,请求出线段CE的长度.

【答案】(1)△AFC是等腰三角形.(2)CE=2.5.
【解析】
试题分析:(1)由矩形的性质可知AD∥BC,从而得到∠FAC=∠ACB,由翻折的性质可知∠ACB=∠ACF,于是得到∠FAC=∠FCA,故此可得到△AFC为等腰三角形;
(2)先依据勾股定理求得AC=5,由翻折的性质可知BE=EF,AF=AB=3,可求得FC=2,设EC=x,则BE=EF=4﹣x,最后在△EFC中由勾股定理可求得EC的长.
解:(1)∵四边形ABCD为矩形,
∴AD∥BC.
∴∠FAC=∠ACB.
由翻折的性质可知;∠ACB=∠ACF,
∴∠FAC=∠FCA.
∴AF=FC.
∴△AFC是等腰三角形.
(2)在Rt△ABC中,由勾股定理得:AC=![]() =5.
=5.
∵由翻折的性质可知:BE=EF,AF=AB=3.
∴FC=2,设EC=x,则BE=EF=4﹣x.
在Rt△EFC中,由勾股定理可知;EF2+FC2=EC2,即(x﹣4)2+22=x2.
解得:x=2.5.
∴CE=2.5.

练习册系列答案
相关题目