题目内容
【题目】如图,在平面直角坐标系xOy中,点A在y轴上,点B在x轴上,∠ABO=60°,若点D(1,0)且BD=2OD.把△ABO绕着点D逆时针旋转m°(0<m<180)后,点B恰好落在初始Rt△ABO的边上,此时的点B记为B′,则点B′的坐标为 .

【答案】(2,![]() )或(0,
)或(0,![]() ).
).
【解析】
试题分析:分类讨论:当点B恰好落在AB上,如图1,根据旋转的性质得DB=DB′=2,易得△DBB′为等边三角形,作B′E⊥DB于E,如图1,根据等边三角形的性质得DE=BE=![]() BD=1,B′E=
BD=1,B′E=![]() DE=
DE=![]() ,则B′(2,
,则B′(2,![]() );当点B恰好落在OA上,如图1,根据旋转的性质得DB=DB′=2,利用勾股定理计算出OB′=
);当点B恰好落在OA上,如图1,根据旋转的性质得DB=DB′=2,利用勾股定理计算出OB′=![]() ,则B′(0,
,则B′(0,![]() ),于是得到B′点的坐标为(2,
),于是得到B′点的坐标为(2,![]() )或(0,
)或(0,![]() ).
).
解:∵点D(1,0)且BD=2OD,
∴BD=2,
当把△ABO绕着点D逆时针旋转m°(0<m<180)后得到△A′B′C′,点B恰好落在AB上,如图1,
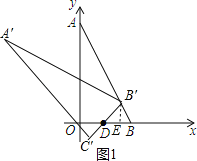
∴DB=DB′,
而∠ABO=60°,
∴△DBB′为等边三角形,
作B′E⊥DB于E,如图1,
∴DE=BE=![]() BD=1,B′E=
BD=1,B′E=![]() DE=
DE=![]() ,
,
∴B′(2,![]() );
);
当把△ABO绕着点D逆时针旋转m°(0<m<180)后得到△A′B′C′,点B恰好落在OA上,如图2,
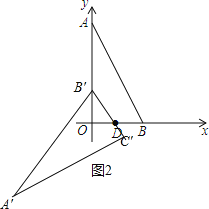
∴DB=DB′=2,
∴OB′=![]() =
=![]() ,
,
∴B′(0,![]() ).
).
故答案为(2,![]() )或(0,
)或(0,![]() ).
).

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
