Question

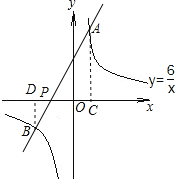
【题目】在平面直角坐标系xOy中，反比例函数y=的图象过点A（1，6）．

（1）求反比例函数的表达式；

（2）过点A的直线与反比例函数y=图象的另一个交点为B，与x轴交于点P，若AP=2PB，求点P的坐标．

Answer 1

【答案】（1）y=；（2）P（﹣1，0）．

【解析】

试题分析：（1）把A点代入，根据待定系数法即可求得；

（2）作AC⊥x轴于C，BD⊥x轴于D，通过证得△APC∽△BPD，得出==2，求得B的纵坐标，代入解析式求得坐标，然后根据待定系数法求得直线AB的解析式，令y=0，即可求得P的坐标．

解：（1）∵反比例函数y=的图象过点A（1，6），

∴k=1×6=6，

∴反比例函数的表达式为：y=；

（2）作AC⊥x轴于C，BD⊥x轴于D，

∵AC∥BD，

∴△APC∽△BPD，

∴=，

∵AP=2PB，

∴AC=2BD，

∵AC=6，

∴BD=3，

∴B的纵坐标为﹣3，

代入y=得，﹣3=，解得x=﹣2，

∴B（﹣2，﹣3），

设直线AB的解析式为y=kx+b，

∴，解得，

∴直线AB的解析式为y=3x+3，

令y=0，则求得x=﹣1，

∴P（﹣1，0）．