Question

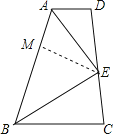
【题目】已知四边形ABCD中，E是CD上的一点连接AE、BE，如图给出四个条件：①AE平分∠BAD，②BE平分∠ABC，③AE⊥EB，④AB=AD+BC，请你以其中三个作为命题的条件，写出一个能推出AD∥BC的正确命题，并加以证明．

Answer 1

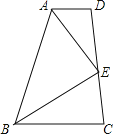
【答案】①②④推出AD∥BC

【解析】

根据①②④能推出AD∥BC，在AB上取点M，使AM=AD，连结EM，证△AME≌△ADE和△BME≌△BCE，求出∠D=∠AME，∠C=∠BME，推出∠D+∠C=180°，根据平行线的判定得出即可．

如：①②④推出AD∥BC，

证明：在AB上取点M，使AM=AD，连结EM，

∵AE平分∠BAD，

∴∠MAE=∠DAE，

在△AEM和△AED中，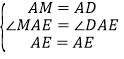

∴△AEM≌△AED（SAS），

∴∠D=∠AME，

又∵AB=AD+BC，

∴MB=BC，

在△BEM和△BCE中，

，

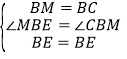∴△BEM≌△BCE（SAS），

∴∠C=∠BME，

∴∠D+∠C=∠AME+∠BME=180°，

∴AD∥BC．