题目内容
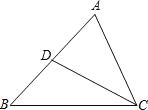
【题目】如图,E,F,G,H分别是边AB,BC,CD,DA的中点.
(1)判断四边形EFGH的形状,并证明你的结论;
(2)当BD,AC满足什么条件时,四边形EFGH是正方形.(不要求证明)

【答案】(1) 四边形EFGH是平行四边形,证明见解析;(2) 当BD=AC且BD⊥AC时,四边形EFGH是正方形.
【解析】试题分析:(1)、根据三角形中位线的性质得出EF∥HG,且EF=HG,从而得出平行四边形;(2)、要使邻边相等则需要满足BD=AC,要使有一个角为直角则需要满足BD⊥AC,从而得出正方形.
试题解析:(1)、四边形EFGH是平行四边形.
∵E,F分别是边AB、BC的中点,∴EF∥AC, 且EF=![]() AC
AC
同理:HG∥AC,且HG=![]() AC ∴EF∥HG,且EF=HG.∴四边形EFGH是平行四边形.
AC ∴EF∥HG,且EF=HG.∴四边形EFGH是平行四边形.
(2)、当BD=AC且BD⊥AC时,四边形EFGH是正方形.

 寒假天地重庆出版社系列答案
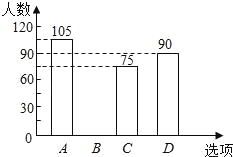
寒假天地重庆出版社系列答案【题目】某校在民族团结宣传活动中,采用了四种宣传形式:A唱歌,B舞蹈,C朗诵,D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:
选项 | 方式 | 百分比 |
A | 唱歌 | 35% |
B | 舞蹈 | a |
C | 朗诵 | 25% |
D | 器乐 | 30% |
请结合统计图表,回答下列问题:
(1)本次调查的学生共 人,a= ,并将条形统计图补充完整;
(2)如果该校学生有2000人,请你估计该校喜欢“唱歌”这种宣传形式的学生约有多少人?
(3)学校采用调查方式让每班在A、B、C、D四种宣传形式中,随机抽取两种进行展示,请用树状图或列表法,求某班抽到的两种形式恰好是“唱歌”和“舞蹈”的概率.
【题目】某次体育测试后,12名九年级学生的成绩如下表所示,这这组数据的众数和中位数分别是()
成绩 | 68 | 67 | 69.5 | 70 | 69 |
人数 | 2 | 1 | 2 | 3 | 4 |
A. 69,69.5 B. 69,69 C. 70,69 D. 69,70