题目内容
【题目】如图,在△ABC中,CD是AB边上的中线,已知∠B=45°,tan∠ACB=3,AC=![]() ,求:
,求:
(1)△ABC的面积;
(2)sin∠ACD的值.
【答案】(1)6;(2)![]() .
.
【解析】
试题分析:(1)作AH⊥BC于H,如图,在Rt△ACE中,利用正切的定义得到tan∠ACE=![]() =3,则设CH=x,AH=3x,根据勾股定理得AC=
=3,则设CH=x,AH=3x,根据勾股定理得AC=![]() x,利用
x,利用![]() x=
x=![]() ,解得x=1,再在Rt△ABH中,利用∠B=45°得到BH=AH=3,然后根据三角形面积公式求解;
,解得x=1,再在Rt△ABH中,利用∠B=45°得到BH=AH=3,然后根据三角形面积公式求解;
(2)作DF⊥BC于F,如图,由于CD是AB边上的中线,根据三角形面积公式得到S△ACD=S△ABC=6,再证明DF为△AB的中位线,则DF=![]() AH=
AH=![]() ,易得BF=DF=
,易得BF=DF=![]() ,接着根据勾股定理计算出CD=
,接着根据勾股定理计算出CD=![]() ,然后利用锐角三角函数得出sin∠ACD的值.
,然后利用锐角三角函数得出sin∠ACD的值.
试题解析:(1)如图,
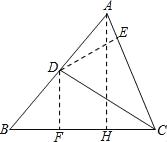
(1)作AH⊥BC于H,
在Rt△ACH中,
∵tan∠ACB=3,AC=![]() ,
,
设CH=x,AH=3x,
根据勾股定理得AC=![]() x,
x,
∴CH=1,AH=3,
在Rt△ABH中,∠B=45°,
∴BH=AH=3,
∴S△ABC=![]() ×4×3=6;
×4×3=6;
(2)作DF⊥BC于F,
∵S△ACD=![]() ×
×![]() ×DE=3,
×DE=3,
∴DE=![]() ,
,
∵AH⊥BC,DF⊥BC,CD是AB边上的中线,
∴DF=![]() AH=
AH=![]() ,
,
∴BF=DF=![]() ,
,
在Rt△CDF中,CD=![]() ,
,
∴在Rt△CDE中,sin∠ACD=![]() .
.

练习册系列答案
相关题目
【题目】某市某一周的PM2.5(大气中直径小于等于2.5微米的颗粒物,也称可入肺颗粒物指数如表,则该周PM2.5指数的众数和中位数分别是________
PM2.5指数 | 150 | 155 | 160 | 165 |
天 数 | 3 | 2 | 1 | 1 |
