题目内容
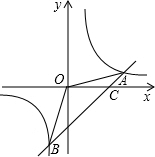
如图,直线y1=2x与双曲线y2=
相交于点A、E.另一直线y3=x+b与双曲线交于点A、B,与x、y 轴分别交于点C、D.直线EB交x轴于点F.
轴分别交于点C、D.直线EB交x轴于点F.
(1)求A、B两点的坐标,并比较线段OA、OB的长短;
(2)由函数图象直接写出函数y2>y3>y1的自变量x的取值范围;
(3)求证:△COD∽△CBF.
| 8 |
| x |
 轴分别交于点C、D.直线EB交x轴于点F.
轴分别交于点C、D.直线EB交x轴于点F.(1)求A、B两点的坐标,并比较线段OA、OB的长短;
(2)由函数图象直接写出函数y2>y3>y1的自变量x的取值范围;
(3)求证:△COD∽△CBF.
(1)由题意得:
,
解得
,或
,
∴A(-2,-4),E(2,4),
将A坐标代入y3=x+b中,得b=-2,即y3=x-2,
联立得:
解得:
,
∴B(4,2);
OA=
,OB=
,
∴AO=BO,
(2)∵A点坐标为(-2,-4),
∴结合图象当x<-2时,y2>y3>y1;
(3)设直线EB的解析式为y=k1x+b1,直线AB的解析式为y=k2x+b2,
则有
,
,
解得:
,
∵k1•k2=-1,
∴AB⊥EF,∴∠CBF=∠DOC=90°
∵∠OCD=∠BCF,
∴△DOC∽△CBF.
|
解得
|
|
∴A(-2,-4),E(2,4),
将A坐标代入y3=x+b中,得b=-2,即y3=x-2,
联立得:
|
解得:
|
∴B(4,2);
OA=
| 22+42 |
| 22+42 |
∴AO=BO,
(2)∵A点坐标为(-2,-4),
∴结合图象当x<-2时,y2>y3>y1;
(3)设直线EB的解析式为y=k1x+b1,直线AB的解析式为y=k2x+b2,
则有
|
|
解得:
|
|
∵k1•k2=-1,
∴AB⊥EF,∴∠CBF=∠DOC=90°
∵∠OCD=∠BCF,
∴△DOC∽△CBF.

练习册系列答案
相关题目
 两点,连接OA、OB.
两点,连接OA、OB.
 比例函数
比例函数

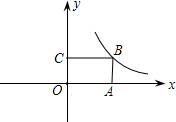 OA:0C=2:1.
OA:0C=2:1.