题目内容
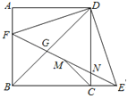
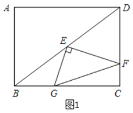
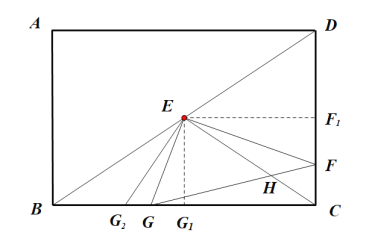
【题目】如图1,在矩形ABCD中,AB=6,BC=8,点E是对角线BD的中点,直角∠GEF的两直角边EF、EG分别交CD、BC于点F、G.
(1)若点F是边CD的中点,求EG的长;
(2)当直角∠GEF绕直角顶点E旋转,旋转过程中与边CD、BC交于点F、G.∠EFG的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠EFG的值;
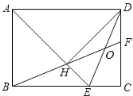
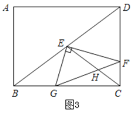
(3)如图3,连接CE交FG于点H,若![]() ,请求出CF的长.
,请求出CF的长.

【答案】(1)3;(2)∠EFG的大小不发生变化,理由见详解;![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据点E是对角线BD的中点,点F是边CD的中点,可证![]() ,再根据
,再根据![]() 可得四边形EGCF是矩形,则点G是边BC的中点,可求出EG;
可得四边形EGCF是矩形,则点G是边BC的中点,可求出EG;
(2)作![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,可得
,可得![]() 是
是![]() 绕直角顶点E旋转而得到的,利用
绕直角顶点E旋转而得到的,利用![]() ,
,![]() ,易证
,易证![]() ,根据相似比
,根据相似比![]() 可得
可得![]() ,则有
,则有![]() ,可知
,可知![]() 的大小在转动的过程中不会发生变化;利用
的大小在转动的过程中不会发生变化;利用![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,则
,则![]() ;
;
(3)连接CE交FG于点H,作![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,过点E作
,过点E作![]() 交
交![]() 于
于![]() ,则
,则![]() 是
是![]() 绕直角顶点E旋转而得到的,由(2)知
绕直角顶点E旋转而得到的,由(2)知![]() 的大小在转动的过程中不会发生变化,易证
的大小在转动的过程中不会发生变化,易证![]() ,则
,则![]() ,有
,有![]() ,可得
,可得![]() ,设
,设![]() ,则
,则![]() ,可求得
,可求得![]() ,
,![]() ,利用勾股定理即可求出
,利用勾股定理即可求出![]() 的值,即可得到
的值,即可得到![]() 的值.
的值.
解:(1)如图示,

∵点E是对角线BD的中点,点F是边CD的中点,
∴![]() ,
,
∵![]() ,
,
∴![]()
∴四边形EGCF是矩形,
∴![]() ,
,
∴点G是边BC的中点,
∴![]() ;
;
(2)答:∠EFG的大小不会发生变化。
证明:如图示:作![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,连接
,连接![]()
∴![]() ,
,![]() ,
,
∴![]() 是
是![]() 绕直角顶点E旋转而得到的,
绕直角顶点E旋转而得到的,
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]() 的大小在转动的过程中不会发生变化;
的大小在转动的过程中不会发生变化;
∵点E是对角线BD的中点,![]() ,
,![]() ,
,
∴![]() ,
,![]()
∴![]()
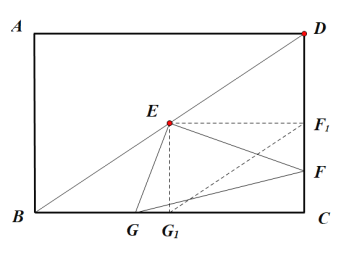
(3)如图示,连接CE交FG于点H,作![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,过点E作
,过点E作![]() 交
交![]() 于
于![]() ,
,
则![]() 是
是![]() 绕直角顶点E旋转而得到的,
绕直角顶点E旋转而得到的,
∴![]()
又∵![]()
∴![]()
∴![]()
∴![]()
∴![]() ,即:
,即:![]() ,
,
设![]() ,则
,则![]() ,
,
由(2)可知:![]() ,
,![]() ,
,![]()
∴![]() ,即:
,即:![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
即:![]() ,解之得:
,解之得:![]() (取正值),
(取正值),
即:![]() .
.