题目内容
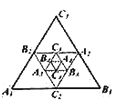
【题目】如图，小红作出了边长为1的第1个等边
，算出了等边的面积，然后分别取三边的中点
、
、
，作出了第2个等边
，算出了等边的面积，用同样的方法，作出了第3个等边
，算出了等边的面积……，由此可得，第
个等边
的面积是（ ）
A.
B.
C.
D.
【答案】C
【解析】
根据相似三角形的性质，先求出正△A2B2C2，正△A3B3C3的面积，依此类推第n个等边△AnBnCn的面积是
.
解：第一个等边△A1B1C1的面积是：
，
∵△A2B2C2与△A1B1C1相似，并且相似比是1：2，
∴面积的比是1：4，
则第二个等边△A2B2C2的面积是
；
∵等边△A3B3C3与等边△A2B2C2的面积的比也是1：4，
∴第三个等边△A3B3C3面积是
；
依此类推△AnBnCn与△An-1Bn-1Cn-1的面积的比是1：4，
第n个三角形的面积是，
故选：C．
练习册系列答案
阅读快车系列答案
相关题目
