Question

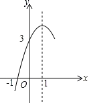
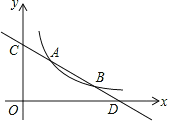
【题目】如图，在平面直角坐标系中，OA⊥OB，AB⊥x轴于点C，点A（，1）在反比例函数y=的图像上.

（1）求反比例函数y=的表达式；

（2）在x轴上是否存在一点P，使得SΔAOP=SΔAOB，若存在求点P的坐标；若不存在请说明理由.

（3）若将ΔBOA绕点B按逆时针方向旋转60°得到ΔBDE，直接写出点E的坐标，并判断点E是否在该反比例函数的图象上，说明理由.

Answer 1

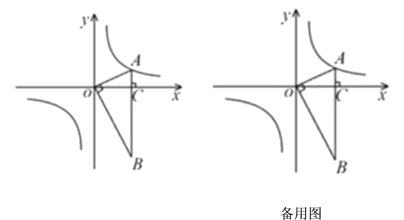
【答案】（1）y=；（2）P（-2，0）或（2，0）；（3）E（-，-1），点E在反比例函数y=的图像上.

【解析】

（1）将点A（，1）代入y=，利用待定系数法即可求出反比例函数的表达式；

（2）先由射影定理求出BC=3，那么AB=4，计算求出S△AOB，进而求出S△AOP．设点P的坐标为（m，0），列出方程求解即可；

（3）先解△OAB，得出∠ABO=30°，再根据旋转的性质求出E点坐标为（-，-1），即可求解．

（1）∵点A（，1）在反比例函数y=的图像上，

∴k=×1=，

∴y=；

（2）∵A（，1），

∴OC=，AC=1，

由△OAC∽△BOC得OC2=ACBC可得BC=3，

∴BA=4，

∴SΔAOB=××4=2，

∵SΔAOP=SΔAOB

∴SΔAOP=，

设P（m，0）

∴××1=，

∴=2，

∴m=-2或2，

∴P（-2，0）或（2，0） ；

（3）E（-，-1），点E在反比例函数y=的图像上，

点E在该反比例函数的图象上，理由如下：
∵OA⊥OB，OA=2，OB=2，AB=4，

∴sin∠ABO=，

∴∠ABO=30°，

∵将△BOA绕点B按逆时针方向旋转60°得到△BDE，

∴△BOA≌△BDE，∠OBD=60°，

∴BO=BD=2，OA=DE=2，∠BOA=∠BDE=90°，∠ABD=30°+60°=90°，

而BD-OC=，BC-DE=1，

∴E（-，-1），

∵-×（-1）=，

∴点E在该反比例函数的图象上．