Question

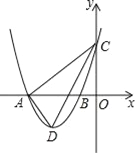
【题目】如图1，抛物线的顶点A的坐标为（1，4），抛物线与x轴相交于B，C两点，与y轴交于点D（0，3）．

（1）求抛物线的表达式以及点B的坐标；

（2）在抛物线的对称轴上是否存在一点P，使得DP+CP最小，如果存在，求出点P的坐标；如果不存在，请说明理由．

（3）点Q是线段BD上方抛物线上的一个动点．过点Q作x轴的垂线，交线段BD于点E，再过点Q作QF∥x轴交抛物线于点F，连结EF，请问是否存在点Q使△QEF为等腰直角三角形？若存在，求出点Q的坐标；若不存在，说明理由．

Answer 1

【答案】（1）y＝﹣x2+2x+3；B的坐标是（3，0）；（2）存在，P的坐标是（1，2）；（3）存在，点Q的坐标为（2，3）或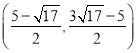

【解析】

（1）根据顶点坐标，则设顶点式，代入点C的坐标即可求出抛物线的解析式；令y=0，求得x的值，从而得到点B的坐标；

（2）根据轴对称的最短路径问题，连接DB交对称轴于P，此时PD+PB=PD+PC的值最小，先求E'F的解析式，它与对称轴的交点就是所求的点G；

（3）设Q（n，﹣n2+2n+3），则E（n，﹣n+3），F（﹣n+2，﹣n2+2n+3），所以可以用的代数式表示QE和QF的长，由题意得QE＝QF即﹣n2+3n＝|2n﹣2|，即可求得符合题意的的值，从而求得点Q的坐标.

（1）∵抛物线的顶点A的坐标为（1，4），

∴设抛物线的表达式为：y＝a（x﹣1）2+4，

把（0，3）代入得：3＝a（0﹣1）2+4，a＝﹣1，

∴抛物线的表达式为：y＝﹣（x﹣1）2+4＝﹣x2+2x+3；

令y＝0，﹣（x﹣1）2+4＝0，解得x1＝3，x2＝﹣1，

∴B的坐标是（3，0），C的坐标是（﹣1，0）；

（2）存在，

如图1，因为B，C关于对称轴对称，连接BD交对称轴于P，此时DP+CP的值最小，

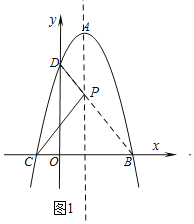
∵D（0，3），B（3，0），易得BD的解析式为：y＝﹣x+3，

当x＝1时，y＝﹣1+3＝2，

∴P的坐标是（1，2）；

（3）如图2，存在点Q，使△QEF为等腰直角三角形，

设Q（n，﹣n2+2n+3），则E（n，﹣n+3），F（﹣n+2，﹣n2+2n+3），

∴QE＝（﹣n2+2n+3）﹣（﹣n+3）＝﹣n2+3n，QF＝|2n﹣2|，

∵QE⊥x轴、QF∥x轴，

∴∠EQF＝90°，

∴当QE＝QF时，△QEF为等腰直角三角形，即：﹣n2+3n＝|2n﹣2|，

①﹣n2+3n＝2n﹣2，即:,即：

解得：n1＝﹣1（不合题意，舍去），n2＝2，

则Q（2，3）；

②﹣n2+3n＝﹣2n+2，即：,

解得：n1＝＞3（不合题意，舍去），n2＝，

则Q（，）．

综上，点Q的坐标为（2，3）或（，）