Question

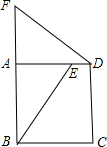四边形ABCD是正方形，△ABE绕点A按逆时针方向旋转了90°得到了△ADF，若DE=3，BF=11，则ABCD的面积为

1. A.
   49
2. B.
   36
3. C.
   25
4. D.
   16

Answer 1

A
分析：由△ABE绕点A按逆时针方向旋转了90°得到了△ADF，根据旋转的性质得到AF=AE，设正方形ABCD的边长为a，则AF=AE=AD-DE=a-3，得到AF+AB=a-3+a=11，即可求得a，然后根据正方形的面积公式计算出ABCD的面积．
解答：∵△ABE绕点A按逆时针方向旋转了90°得到了△ADF，
∴AF=AE，
设正方形ABCD的边长为a，
∴AF=AE=AD-DE=a-3，
∴AF+AB=a-3+a=11，
∴a=7，
∴正方形ABCD的面积=a²=7²=49．
故选A．
点评：本题考查了旋转的性质：旋转前后两图形全等，对应点到旋转中心的距离相等，对应点与旋转中心连线段的夹角等于旋转角．也考查了正方形的性质．