题目内容
【题目】如图,在△ABC中,AB=AC=2,∠BAC=20°.动点P、Q分别在直线BC上运动,且始终保持∠PAQ=100°.设BP=x,CQ=y,则y与x之间的函数关系用图象大致可以表示为( )

A. 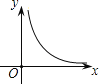 B.
B. 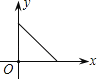 C.
C.  D.
D. 
【答案】A
【解析】
试题分析:根据△ABC是等腰三角形,∠BAC=20°,则∠ABC=∠ACB=80°.根据三角形的外角等于不相邻的两内角的和,得到∠QAC=∠P,得到△APB∽△QAC,根据相似三角形的对应边的比相等,即可求得x与y的函数关系式,即可进行判断.∵△ABC中,AB=AC,∠BAC=20° ∴∠ACB=80°
又∵∠PAQ=∠PAB+∠BAC+∠CAQ=100° ∴∠PAB+∠CAQ=80° 在△ABC中:∠ACB=∠CAQ+∠AQC=80°
∴∠AQC=∠PAB 同理:∠P=∠CAQ ∴△APB∽△QAC ∴![]() ,即
,即![]() . 则函数解析式是y=
. 则函数解析式是y=![]() .
.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目