题目内容
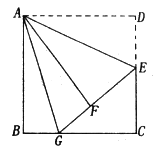
【题目】已知：如图，在边长为8的正方形ABCD中，E是边CD的中点，将
沿AE对折至
，延长EF交边BC于点G，连接AG。
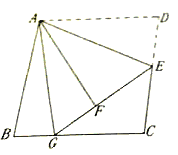
（1）求证：
； （2）求BG的长。
【答案】（1）、证明过程见解析；（2）、
【解析】
试题分析：（1）、根据折叠图形的性质得出AD=AF，BE=EF，∠D＝∠AFE＝90°，从而得出AB=AF，∠B＝∠AFG＝90°，结合AG为公共边，利用HL判定定理得出三角形全等；（2）、设BG=FG=x，则GC=8-x，根据中点的性质得出EG=4+x，根据Rt△CEG的勾股定理求出x的值，得出答案.
试题解析：（1）、在正方形ABCD中，
，∠D＝∠B＝∠BCD＝90°
∵将△ADE沿AE对折至△AFE， 
，∠D＝∠AFE＝90°，
，∠B＝∠AFG＝90° 又
， ∴△ABG≌△AFG（HL）
（2）、∵△ABG≌△AFG，
， 设
，则
，
∵E为CD的中点，
，
∴在Rt△CEG中，
，解得
， 
练习册系列答案
相关题目
