题目内容
已知等腰三角形的两条边分别为5，6，求一腰上的高线长．
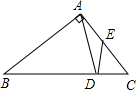
△ABC中，AB=AC，
设AD=x，
分为两种情况：①当AB=AC=5，BC=6时，
则CD=5-x，
∵在Rt△ABD和Rt△CDB中，由勾股定理得：BD2=AB2-AD2=BC2-CD2，
∴52-x2=62-（5-x）2，
x=
| 7 |
| 5 |
∴BD2=52-（
| 7 |
| 5 |
∴BD=
| 24 |
| 5 |
②当AB=AC=6，BC=5时，
则CD=6-x，
∵在Rt△ABD和Rt△CDB中，由勾股定理得：BD2=AB2-AD2=BC2-CD2，
∴62-x2=52-（6-x）2，
x=
| 47 |
| 12 |
∴BD2=62-（
| 47 |
| 12 |
∴BD=
35
| ||
| 12 |
即一腰上的高线长是
| 24 |
| 5 |
35
| ||
| 12 |
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
弧法”，如图所示，方法是：
