题目内容
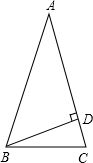
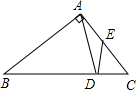
如图，等腰三角形ABC中，∠BAC=90°，在底边BC上截取BD=AB，过D作DE⊥BC交AC于E，连接AD，则图中等腰三角形的个数是（ ）
| A．1 | B．2 | C．3 | D．4 |
∵三角形ABC是等腰三角形，且∠BAC=90°，
∴∠B=∠C=45°，
∵DE⊥BC，
∴∠EDB=∠EDC=90°
∴∠DEC=∠C=45°，
∴△EDC是等腰三角形，
∵BD=AB，
∴△ABD是等腰三角形，
∴∠BAD=∠BDA，
而∠EAD=90°-∠BAD，∠EDA=90°-∠BDA，
∴∠EAD=∠EDA，
∴△EAD是等腰三角形，
因此图中等腰三角形共4个．
故选D．
∴∠B=∠C=45°，
∵DE⊥BC，
∴∠EDB=∠EDC=90°
∴∠DEC=∠C=45°，
∴△EDC是等腰三角形，
∵BD=AB，
∴△ABD是等腰三角形，
∴∠BAD=∠BDA，
而∠EAD=90°-∠BAD，∠EDA=90°-∠BDA，
∴∠EAD=∠EDA，
∴△EAD是等腰三角形，
因此图中等腰三角形共4个．
故选D．
练习册系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
