题目内容
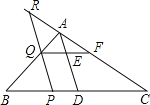
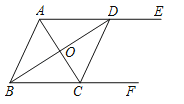
【题目】已知等边△ABC的重心为G,△DEF与△ABC关于点G成中心对称,将它们重叠部分的面积记作S1,△ABC的面积记作S2,那么![]() 的值是_____
的值是_____
【答案】![]()
【解析】
如图,根据点G是等边△ABC的重心,得到AD垂直平分BC,AD是∠BAC的角平分线,根据中心对称的性质得到△DEF≌△ABC,AG=DG,EF∥BC,推出△AQH是等边三角形,得到AQ=HQ=AH,求得它们重叠部分为边长=QH的正六边形,设AB=3a,则QH=a,根据等边三角形的面积即可得到结论.
解:如图,

∵点G是等边△ABC的重心,
∴AD垂直平分BC,AD是∠BAC的角平分线,
∴AG=2GN,
设AB=3a,则AN=![]() ×3a=
×3a=![]() a,
a,
∵△DEF与△ABC关于点G成中心对称,
∴△DEF≌△ABC,AG=DG,EF∥BC,
∴∠AQH=∠ABC=∠AHQ=∠ACB=60°,
∴△AQH是等边三角形,
∴AQ=HQ=AH=![]() AB=a,
AB=a,
∴AP=![]() a,
a,
∴它们重叠部分为边长=QH的正六边形,
∴S1=![]() ,S2=
,S2=![]() ,
,
∴![]() =
=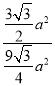 =
=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目