题目内容
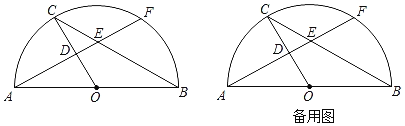
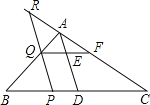
【题目】已知三角形ABC,AD为BC边中线,P为BC上一动点,过点P作AD的平行线,交直线AB或延长线于点Q,交CA或延长线于点R.
(1)当点P在BD上运动时,过点Q作BC的平行线交AD于E点,交AC于F点,求证:QE=EF;
(2)当点P在BC上运动时,求证:PQ+PR为定值.
【答案】(1)证明见解析;(2)证明见解析
【解析】
(1)根据平行线QF∥BC,可以推知△AQE∽△ABD,△AEF∽△ADC;然后根据相似三角形的对应边成比例可求得![]() ;再根据已知条件“AD为BC边中线”来证明QE=EF;
;再根据已知条件“AD为BC边中线”来证明QE=EF;
(2)分类讨论:
①当点P与点B(或点C)重合时,AD为△B(P)RC(或△C(P)BQ)的中位线,PQ+PR=2AD;
②当点P在BD上(不与点B重合)运动时,由(1)证明可知,AE为△RQF的中位线,PQ+PR=2AD;
③当点P在CD上(不与点C重合)运动时,PQ+PR=2AD.
(1)证明:∵QF∥BC,
∴△AQE∽△ABD,△AEF∽△ADC.
∴![]() ,
,
∵BD=DC,
∴QE=EF.
(2)解:当点P与点B(或点C)重合时,AD为△B(P)RC(或△C(P)BQ)的中位线,
∴PQ+PR=2AD.
当点P在BD上(不与点B重合)运动时,由(1)证明可知,AE为△RQF的中位线,
∴RQ=2AE.
∵QF∥BC,PQ∥AD,
∴四边形PQED为平行四边形.
∴PQ=DE,
∴PQ+PR=2DE+QR=2DE+2AE=2AD.
同理可证,当点P在CD上(不与点C重合)运动时,
PQ+PR=2AD.
∴P在BC上运动时,PQ+PR为定值,
即PQ+PR=2AD.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案【题目】某单位计划购进![]() 三种型号的礼品共
三种型号的礼品共![]() 件,其中
件,其中![]() 型号礼品
型号礼品![]() 件,
件,![]() 型号礼品比
型号礼品比![]() 型号礼品多
型号礼品多![]() 件.已知三种型号礼品的单价如下表:
件.已知三种型号礼品的单价如下表:
型号 |
|
|
|
单价(元/件) |
|
|
|
(1)求计划购进![]() 和
和![]() 两种型号礼品分别多少件?
两种型号礼品分别多少件?
(2)实际购买时,厂家给予打折优惠销售(如: ![]() 折指原价
折指原价![]() ,在计划总价额不变的情况下,准备购进这批礼品.
,在计划总价额不变的情况下,准备购进这批礼品.
①若只购进![]() 两种型号礼品,且
两种型号礼品,且![]() 型礼品件数不超过
型礼品件数不超过![]() 型礼品的
型礼品的![]() 倍,求
倍,求![]() 型礼品最多购进多少件?
型礼品最多购进多少件?
②若只购进![]() 两种型号礼品,它们的单价分别打
两种型号礼品,它们的单价分别打![]() 折、
折、![]() 折,
折,![]() 均为整数,且购进的礼品总数比计划多
均为整数,且购进的礼品总数比计划多![]() 件,求
件,求![]() 的值.
的值.