题目内容
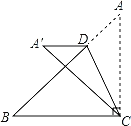
【题目】如图,已知二次函数y=x2﹣2x+m的图象与x轴交于点A、B,与y轴交于点C,直线AC交二次函数图象的对称轴于点D,若点C为AD的中点.
(1)求m的值;
(2)若二次函数图象上有一点Q,使得tan∠ABQ=3,求点Q的坐标;
(3)对于(2)中的Q点,在二次函数图象上是否存在点P,使得△QBP∽△COA?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)m=﹣3;(2)Q(﹣4,21)或(2,﹣3);(3)不存在,理由见解析
【解析】
(1)函数的对称轴为:x=1,点C为AD的中点,则点A(-1,0),即可求解;
(2)tan∠ABQ=3,点B(3,0),则AQ所在的直线为:y=±3x(x-3),即可求解;
(3)分点Q(2,-3)、点Q(-4,21)两种情况,分别求解即可.
(1)设对称轴交x轴于点E,直线AC交抛物线对称轴于点D,
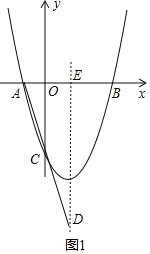
函数的对称轴为:x=1,点C为AD的中点,则点A(﹣1,0),
将点A的坐标代入抛物线表达式并解得:m=﹣3,
故抛物线的表达式为:y=x2﹣2x﹣3…①;
(2)tan∠ABQ=3,点B(3,0),
则AQ所在的直线为:y=±3(x﹣3)…②,
联立①②并解得:x=﹣4或3(舍去)或2,
故点Q(﹣4,21)或(2,﹣3);
(3)不存在,理由:
△QBP∽△COA,则∠QBP=90°
①当点Q(2,﹣3)时,
则BP的表达式为:y=﹣![]() (x﹣3)…③,
(x﹣3)…③,
联立①③并解得:x=3(舍去)或﹣![]() ,故点P(﹣
,故点P(﹣![]() ),
),
此时BP:PQ≠OA:AC,故点P不存在;
②当点Q(﹣4,21)时,
同理可得:点P(﹣![]() ),
),
此时BP:PQ≠OA:OB,故点P不存在;
综上,点P不存在.

 阅读快车系列答案
阅读快车系列答案【题目】某单位计划购进![]() 三种型号的礼品共
三种型号的礼品共![]() 件,其中
件,其中![]() 型号礼品
型号礼品![]() 件,
件,![]() 型号礼品比
型号礼品比![]() 型号礼品多
型号礼品多![]() 件.已知三种型号礼品的单价如下表:
件.已知三种型号礼品的单价如下表:
型号 |
|
|
|
单价(元/件) |
|
|
|
(1)求计划购进![]() 和
和![]() 两种型号礼品分别多少件?
两种型号礼品分别多少件?
(2)实际购买时,厂家给予打折优惠销售(如: ![]() 折指原价
折指原价![]() ,在计划总价额不变的情况下,准备购进这批礼品.
,在计划总价额不变的情况下,准备购进这批礼品.
①若只购进![]() 两种型号礼品,且
两种型号礼品,且![]() 型礼品件数不超过
型礼品件数不超过![]() 型礼品的
型礼品的![]() 倍,求
倍,求![]() 型礼品最多购进多少件?
型礼品最多购进多少件?
②若只购进![]() 两种型号礼品,它们的单价分别打
两种型号礼品,它们的单价分别打![]() 折、
折、![]() 折,
折,![]() 均为整数,且购进的礼品总数比计划多
均为整数,且购进的礼品总数比计划多![]() 件,求
件,求![]() 的值.
的值.
【题目】攀枝花得天独厚,气候宜人,农产品资源极为丰富,其中晚熟芒果远销北上广等大城市.某水果店购进一批优质晚熟芒果,进价为10元/千克,售价不低于15元/千克,且不超过40元/每千克,根据销售情况,发现该芒果在一天内的销售量![]() (千克)与该天的售价
(千克)与该天的售价![]() (元/千克)之间的数量满足如下表所示的一次函数关系.
(元/千克)之间的数量满足如下表所示的一次函数关系.
销售量 | … | 32.5 | 35 | 35.5 | 38 | … |
售价 | … | 27.5 | 25 | 24.5 | 22 | … |
(1)某天这种芒果售价为28元/千克.求当天该芒果的销售量
(2)设某天销售这种芒果获利![]() 元,写出
元,写出![]() 与售价
与售价![]() 之间的函数关系式.如果水果店该天获利400元,那么这天芒果的售价为多少元?
之间的函数关系式.如果水果店该天获利400元,那么这天芒果的售价为多少元?
【题目】某公司为了到高校招聘大学生,为此设置了三项测试:笔试、面试、实习.学生的最终成绩由笔试面试、实习依次按3:2:5的比例确定.公司初选了若干名大学生参加笔试,面试,并对他们的两项成绩分别进行了整理和分析.下面给出了部分信息:
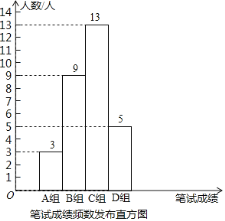
①公司将笔试成绩(百分制)分成了四组,分别为A组:60≤x<70,B组:70≤x<80,C组:80≤x<90,D组:90≤x<100;并绘制了如下的笔试成绩频数分布直方图.其中,C组的分数由低到高依次为:80,81,82,83,83,84,84,85,86,88,88,88,89.
②这些大学生的笔试、面试成绩的平均数、中位数、众数、最高分如下表:
平均数 | 中位数 | 众数 | 最高分 | |
笔试成绩 | 81 | m | 92 | 97 |
面试成绩 | 80.5 | 84 | 86 | 92 |
根据以上信息,回答下列问题:
(1)这批大学生中笔试成绩不低于88分的人数所占百分比为 .
(2)m= 分,若甲同学参加了本次招聘,他的笔试、面试成绩都是83分,那么该同学成绩排名靠前的是 成绩,理由是 .
(3)乙同学也参加了本次招聘,笔试成绩虽不是最高分,但也不错,分数在D组;面试成绩为88分,实习成绩为80分由表格中的统计数据可知乙同学的笔试成绩为 分;若该公司最终录用的最低分数线为86分,请通过计算说明,该同学最终能否被录用?