��Ŀ����
����Ŀ���Ϸ�ij��ҵ����65�����������ס������ֲ�Ʒ��ÿ��ÿ������2����1���ң��ײ�Ʒÿ���ɻ���15Ԫ�������г�������������飬�Ҳ�Ʒÿ�����������5������ÿ������5��ʱ��ÿ���ɻ���120Ԫ��ÿ����1��������ƽ��ÿ���������2Ԫ����ÿ�찲��x�������Ҳ�Ʒ��
(1)������Ϣ�����
��Ʒ���� | ÿ�칤����(��) | ÿ�����(��) | ÿ����Ʒ�ɻ�����(Ԫ) |
�� | _______ | _________ | 15 |
�� | x | x | __________ |
(2)��ÿ�������ײ�Ʒ�ɻ�õ�����������Ҳ�Ʒ�ɻ�õ������550Ԫ����ÿ���Ҳ�Ʒ�ɻ�õ�����
(3)����ҵ�ڲ����ӹ��˵�����£�������������Ʒ��Ҫ��ÿ��ס������ֲ�Ʒ�IJ�����ȣ���֪ÿ��ÿ�������1����(ÿ��ÿ��ֻ������һ����Ʒ)������Ʒÿ���ɻ���30Ԫ����ÿ���������ֲ�Ʒ�ɻ�õ�������W(Ԫ)�����ֵ����Ӧ��xֵ��
���𰸡�(1) 65��x��2(65��x)��130��2x��(2) ÿ���Ҳ�Ʒ�ɻ�õ�������110Ԫ��(3) ����26�������Ҳ�Ʒʱ���ɻ�õ��������Ϊ3198Ԫ
��������
��1������������д������Ϣ���ɣ�
��2�����������г�������⼴�ɣ�
��3���������ײ�Ʒm�ˣ����������г����̿����m=![]() ���ٸ���x��m���ǷǸ��������ɵ�ȡx=26ʱ��m=13��65��x��m=26��
���ٸ���x��m���ǷǸ��������ɵ�ȡx=26ʱ��m=13��65��x��m=26��
��1����һ�� 65��x��2(65��x)���ڶ��� 130��2x��
��2��������15��2(65��x)=x(130��2x)+550,
��x2��80x+700=0
���x1=10��x2=70(�������⣬��ȥ)
��130��2x=110(Ԫ)��
��ÿ���Ҳ�Ʒ�ɻ�õ�������110Ԫ��
��3���������ײ�Ʒm�ˣ�
W=x(130��2x)+15��2m+30(65��x��m)=��2(x��25)2+3200,
��2m=65��x��m
��m=![]() ��
��
��x��m���ǷǸ�����
��ȡx=26ʱ��m=13��65��x��m=26,
����x=26ʱ��W���ֵ=3198��
�𣺰���26�������Ҳ�Ʒʱ���ɻ�õ��������Ϊ3198Ԫ��

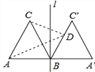
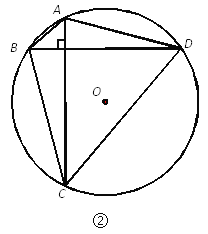
����Ŀ����ͼ���ڡ�ABC�У� ![]() ��
�� ![]() ������D���߶�BC�ϵĶ��㣬���߶�AD�Ƶ�A˳ʱ����ת50����
������D���߶�BC�ϵĶ��㣬���߶�AD�Ƶ�A˳ʱ����ת50����![]() ������
������![]() ����֪AB
����֪AB![]() 2cm����BDΪx cm��B
2cm����BDΪx cm��B![]() Ϊy cm��
Ϊy cm��

С������ѧϰ�����ľ��飬�Ժ���y���Ա���x�ı仯���仯�Ĺ��ɽ�����̽����������С����̽�����̣��벹����������˵���������������ֵ������һλС����
��1��ͨ��ȡ�㡢��ͼ���������õ���![]() ��
��![]() �ļ���ֵ�����±���
�ļ���ֵ�����±���
|
| 0.5 | 0.7 | 1.0 | 1.5 | 2.0 | 2.3 |
| 1.7 | 1.3 | 1.1 | 0.7 | 0.9 | 1.1 |
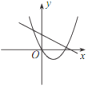
��2������ƽ��ֱ������ϵ������Բ�ȫ��ı��и��Զ�ӦֵΪ����ĵ㣬�����ú�����ͼ��

��3����ϻ����ĺ���ͼ������⣺
�߶�![]() �ij��ȵ���СֵԼΪ__________
�ij��ȵ���СֵԼΪ__________ ![]() ��
��
��![]()
![]() ����
����![]() �ij���x��ȡֵ��Χ��_____________��
�ij���x��ȡֵ��Χ��_____________��