题目内容
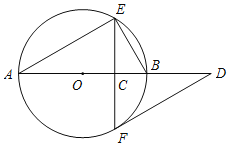
【题目】如图，在平面直角坐标系xOy中，一次函数y＝﹣2x的图象与反比例函数y＝
的图象的一个交点为A(﹣1，n)
(1)求反比例函数y＝的表达式.
(2)若两函数图象的另一交点为B，直接写出B的坐标.
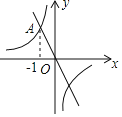
【答案】(1)
；(2)点B的坐标是(1，﹣2).
【解析】
（1）把A的坐标代入y=﹣2x，求出n，得出A的坐标，再把A的坐标代入反比例函数的解析式求出k即可；
（2）根据正比例函数与反比例函数的交点关于原点对称，即可得出答案．
（1）∵点A（﹣1，n）在一次函数y=﹣2x的图象上，∴代入得：n=（﹣2）×（﹣1）=2，∴点A的坐标为（﹣1，2）．
∵点A在反比例函数
的图象上，∴k=（﹣1）×2=﹣2，∴反比例函数的解析式为．
（2）∵正比例函数与反比例函数的交点关于原点对称，∴函数y=﹣2x的图象与反比例函数的图象的另一个交点B的坐标是（1，﹣2）．
【题目】合肥某企业安排65名工人生产甲、乙两种产品，每人每天生产2件甲或1件乙，甲产品每件可获利15元．根据市场需求和生产经验，乙产品每天产量不少于5件，当每天生产5件时，每件可获利120元，每增加1件，当天平均每件利润减少2元．设每天安排x人生产乙产品．
(1)根据信息填表：
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | _______ | _________ | 15 |
乙 | x | x | __________ |
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元，求每件乙产品可获得的利润；
(3)该企业在不增加工人的情况下，增加生产丙产品，要求每天甲、丙两种产品的产量相等．已知每人每天可生产1件丙(每人每天只能生产一件产品)，丙产品每件可获利30元，求每天生产三种产品可获得的总利润W(元)的最大值及相应的x值．
【题目】某市将实行居民生活用电阶梯电价方案，如下表，图中折线反映了每户居民每月电费
（元）与用电量
（度）间的函数关系.
档次 | 第一档 | 第二档 | 第三档 |
每月用电量 |
|
|
|
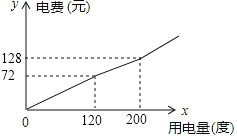
（1）小王家某月用电
度，需交电费___________元；
（2）求第二档电费（元）与用电量（度）之间的函数关系式；
（3）小王家某月用电
度，交纳电费
元，请你求出第三档每度电费比第二档每度电费多多少元？