题目内容
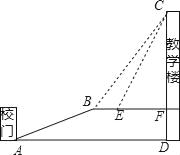
【题目】重庆是一座美丽的山坡,某中学依山而建,校门A处,有一斜坡AB,长度为13米,在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=53°,离B点4米远的E处有一花台,在E处仰望C的仰角∠CEF=63.4°,CF的延长线交校门处的水平面于D点,FD=5米.
(1)求斜坡AB的坡度i.
(2)求DC的长.
(参考数据:tan53°≈![]() ,tan63.4°≈2)
,tan63.4°≈2)
【答案】(1)AB的坡度i=1:2.4;(2)DC=21米.
【解析】
过B作BG⊥AD于G,则四边形BGDF是矩形,求得BG=DF=5米,然后根据勾股定理求得AG,即可求得斜坡AB的坡度i.
在Rt△BCF中,BF=![]() ,在Rt△CEF中,EF=
,在Rt△CEF中,EF=![]() ,得到方程BF-EF=
,得到方程BF-EF=![]() -
-![]() =4,解得CF=16,即可求得求DC=21.
=4,解得CF=16,即可求得求DC=21.
知识点:
坡度:通常把坡面的垂直高度h和水平方向的距离l的比叫做坡度(或叫做坡比)用字母i表示。【即坡角的正切值(可写作:i=tan坡角=h:l)】
正切:把锐角A的对边与邻边的比叫做∠A的正切,记作tanA.
(1)过B作BG⊥AD于G,
则四边形BGDF是矩形,
∴BG=DF=5米,
∵AB=13米,
∴AG=![]() =12米,
=12米,
∴AB的坡度i=![]() =1:2.4;
=1:2.4;
(2)在Rt△BCF中,BF=![]() =
=![]() ,
,
在Rt△CEF中,EF=![]() =
=![]() ,
,
∵BE=4米,
∴BF﹣EF═![]() ﹣
﹣![]() =4,
=4,
解得:CF=16.
∴DC=CF+DF=16+5=21米.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目