题目内容
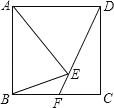
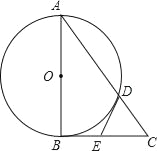
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,点E为BC的中点,连接DE.
(1)求证:DE是⊙O的切线;
(2)求证:4DE2=CDAC.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)如图,作辅助线;根据题意结合图形,证明∠ODE=90°,即可解决问题;
(2)根据圆周角定理得到∠ADB=∠BDC=90°,根据直角三角形的性质得到BC=2DE,根据相似三角形的性质即可得到结论.
(1)证明:连接OD、BD,
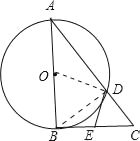
∵AB为⊙O的直径,
∴∠ADB=∠CDB=90°;
又∵点E为BC的中点,
∴BE=DE,
∴∠BDE=∠EBD;
∵OA=OD,
∴∠OAD=∠ODA;
又∵∠OAD+∠OBD=90°,∠EBD+∠OBD=90°,
∴∠OAD=∠EBD,即∠ODA=∠BDE;
∴∠ODE=∠BDE+∠ODB=∠ODA+∠ODB=90°,
又∵点D在⊙O上,
∴DE是圆⊙O的切线;
(2)∵AB为⊙O的直径,
∴∠ADB=∠BDC=90°,
∵点E为BC的中点,
∴BC=2DE,
∵∠ABC=90°,
∴∠ABC=∠BDC,
∵∠C=∠C,
∴△ABC∽△BDC,
∴![]() ,
,
∴BC2=CDAC,
∴4DE2=CDAC.

练习册系列答案
相关题目
【题目】某学校计划在总费用2300元的限额内,租用客车送234名学生和6名教师集体外出活动,每辆客车上至少要有1名教师.现有甲、乙两种大客车,它们的载客量和租金如下表所示.
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 45 | 30 |
租金/(元/辆) | 400 | 280 |
(1)共需租多少辆客车?
(2)请给出最节省费用的租车方案.