题目内容
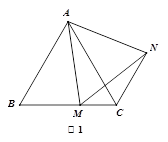
(1)如图1,在等边△ABC中,点M是边BC上的任意一点(不含端点B、C),联结AM,以AM为边作等边△AMN,联结CN.求证:∠ABC=∠ACN.
【类比探究】
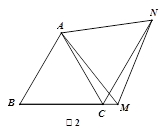
(2)如图2,在等边△ABC中,点M是边BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是边BC上的任意一点(不含端点B、C),联结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.联结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.


【类比探究】
(2)如图2,在等边△ABC中,点M是边BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.

【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是边BC上的任意一点(不含端点B、C),联结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.联结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.

证明见解析.
试题分析:(1)先证△BAM≌△CAN,再由全等三角形性质得到结论;
(2)先证△BAM≌△CAN,再由全等三角形性质得到结论;
(3)先证△ABC∽△AMN,再证△BAM∽△CAN,由相似三角形性质得到结论。
试题解析:(1)∵△ABC、△AMN是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM=∠CAN,
∴△BAM≌△CAN(SAS),
∴∠ABC=∠ACN;
(2)结论∠ABC=∠ACN仍成立.
理由如下:∵△ABC、△AMN是等边三角形,
∴AB=AC,AM=AN,
∠BAC=∠MAN=60°,
∴∠BAM=∠CAN,
∴△BAM≌△CAN(SAS),
∴∠ABC=∠ACN;
(3)∠ABC=∠ACN.
理由如下:
∵BA=BC,MA=MN,顶角∠ABC=∠AMN,
∴底角∠BAC=∠MAN,
∴△ABC∽△AMN,
∴
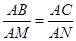 ,
,又∵∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,
∴∠BAM=∠CAN,
∴△BAM∽△CAN,
∴∠ABC=∠ACN.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
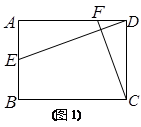
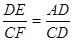 成立?并证明你的结论.
成立?并证明你的结论.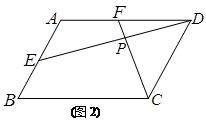

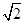 cm,CE="5cm," CD=10cm.
cm,CE="5cm," CD=10cm.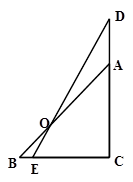
 中,
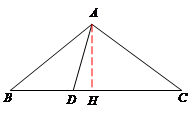
中, ,D是BC上一点,且
,D是BC上一点,且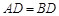 .
.
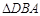 ;
;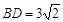 ,
, ,求BC的长;
,求BC的长; ,求
,求 的值.
的值. 、
、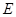 两点分别在
两点分别在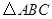 的边
的边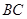 、
、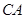 上,
上, 与
与 不平行,当满足条件(写出一个即可) 时,
不平行,当满足条件(写出一个即可) 时,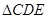 ∽
∽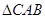 .
.
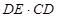
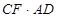 (填“<”或“=”或“>”);
(填“<”或“=”或“>”);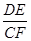 的值为 .
的值为 .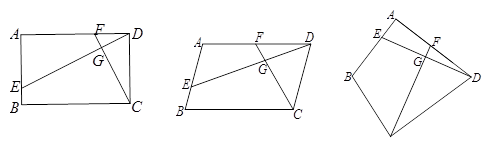
 中,∠
中,∠ °,
°,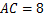 ,
,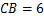 ,在斜边
,在斜边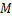 上取一点
上取一点 ,过
,过 交
交 于
于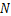 ,则
,则 _______.
_______.
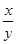 =
=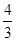 ,那么
,那么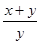 的值是( )
的值是( )