题目内容
四边形ABCD中,点E是AB的中点,F是AD边上的动点.连结DE、CF.
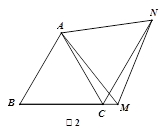
(1)若四边形ABCD是矩形,AD=12,CD=10,如图(1)所示.
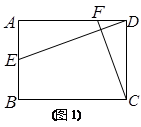
①请直接写出AE的长度;
②当DE⊥CF时,试求出CF长度.
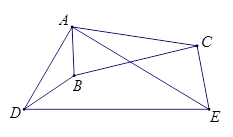
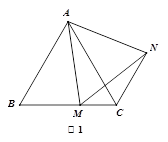
(2)如图(2),若四边形ABCD是平行四边形,DE与CF相交于点P.
探究:当∠B与∠PC满足什么关系时,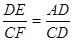 成立?并证明你的结论.
成立?并证明你的结论.
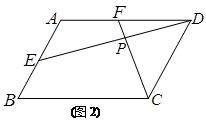
(1)若四边形ABCD是矩形,AD=12,CD=10,如图(1)所示.
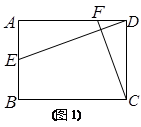
①请直接写出AE的长度;
②当DE⊥CF时,试求出CF长度.
(2)如图(2),若四边形ABCD是平行四边形,DE与CF相交于点P.
探究:当∠B与∠PC满足什么关系时,
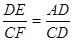 成立?并证明你的结论.
成立?并证明你的结论.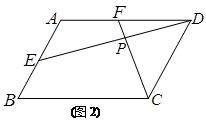
(1)①AE ="5;" ②CF=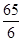 ;
;
(2)当∠B+∠EPC=180°时,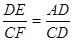 成立.证明见解析.
成立.证明见解析.
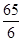 ;
;(2)当∠B+∠EPC=180°时,
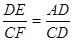 成立.证明见解析.
成立.证明见解析.试题分析:(1) ①四边形ABCD是矩形, CD=10,点E是AB的中点,可得:AE=
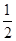 CD=5;
CD=5;②根据已知证得△AED∽△DFC,;利用相似三角形对应边成比例即可;
(2)当∠B+∠EPC=180°时,
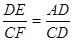 成立.根据已知证得:△DFP∽△DEA,△CPD∽△CDF,再根据对应边成比例即可.
成立.根据已知证得:△DFP∽△DEA,△CPD∽△CDF,再根据对应边成比例即可.试题解析:(1)①∵四边形ABCD是矩形, CD=10,点E是AB的中点,
∴AE=
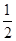 CD=5;
CD=5;②∵四边形ABCD是矩形,
∴∠A=∠FDC=90°,
∵CF⊥DE,
∴∠ADE+∠CFD=90°,∠ADE+∠AED=90°,
∴∠CFD=∠AED,
∵∠A=∠CDF,
∴△AED∽△DFC
∴
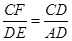
在△AED中,∠A =90°,AD=12,AE =5,
∴
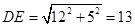
∴
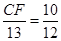
CF=
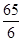 ;
;(2)当∠B+∠EPC=180°时,
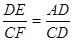 成立.
成立.∵四边形ABCD是平行四边形,
∴∠B=∠ADC,AD∥BC,
∴∠B+∠A=180°,
∵∠B+∠EPC=180°,
∴∠A=∠EPC=∠FPD,
∵∠FDP=∠EDA,
∴△DFP∽△DEA,
∴
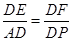 ,
,∵∠B=∠ADC,∠B+∠EPC=180°,∠EPC+∠DPC=180°,
∴∠CPD=∠CDF,
∵∠PCD=∠DCF,
∴△CPD∽△CDF,
∴
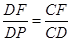 ,
,∴
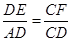 ,
,∴
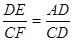 ,
,即当∠B+∠EPC=180°时,
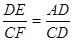 成立.
成立.
练习册系列答案
相关题目
 ,求证:
,求证: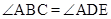 .
. 
 .
.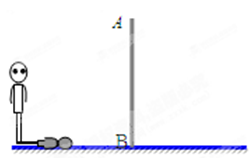
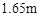 ,在同一时刻测得小丽和建筑物
,在同一时刻测得小丽和建筑物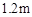 和
和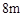 ,求建筑物
,求建筑物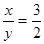 ,则
,则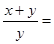 .
.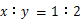 ,则
,则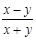 =_____________.
=_____________.

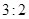 B.
B.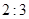 C.
C.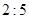 D.
D.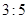
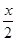 =
=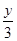 ,那么
,那么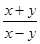 的值是( )
的值是( )