题目内容
如图10,在平面直角坐标系中,正方形OABC边长是4,点A、C分别在y轴、x轴的正半轴上.动点P从点A开始,以每秒2个单位长度的速度在线段AB上来回运动.动点Q从点B开始沿B→C→O的方向,以每秒1个单位长度的速度向点O运动.P、Q两点同时出发,当点Q到达点O时,P、Q两点同时停止运动.设运动时间为t,△OPQ的面积为S.
(1)当t =1时,S = ;
(2)当0≤ t ≤ 2时,求满足△BPQ的面积有最大值的P、Q两点坐标;
(3)在P、Q两点运动的过程中,是否存在某一时刻,使得S = 6.若存在,请直接写出所有符合条件的P点坐标;若不存在,请说明理由.
(1)当t =1时,S = ;
(2)当0≤ t ≤ 2时,求满足△BPQ的面积有最大值的P、Q两点坐标;
(3)在P、Q两点运动的过程中,是否存在某一时刻,使得S = 6.若存在,请直接写出所有符合条件的P点坐标;若不存在,请说明理由.

解:(1)5
(2)由题意可知,当0≤ t ≤ 2时,
PA="2" t,PB="4-2" t, BQ =" t," CQ =" 4-t"
S△BPQ = PB ·BQ = t(4-2 t )="-" t 2+2 t = -(t -1)2 +1
当t =1时,S△BPQ的最大值="1"
此时,P(2,4),Q(4,3)
(3)当0≤ t ≤ 2时,P(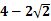 ,4)
,4)
当2< t ≤ 4时,P(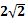 ,4)
,4)
当4< t < 8时,P(2,4)
(2)由题意可知,当0≤ t ≤ 2时,
PA="2" t,PB="4-2" t, BQ =" t," CQ =" 4-t"
S△BPQ = PB ·BQ = t(4-2 t )="-" t 2+2 t = -(t -1)2 +1
当t =1时,S△BPQ的最大值="1"
此时,P(2,4),Q(4,3)
(3)当0≤ t ≤ 2时,P(
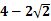 ,4)
,4)当2< t ≤ 4时,P(
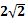 ,4)
,4)当4< t < 8时,P(2,4)
(1)计算当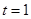 相应线段的长,再从矩形中减去旁边三个三角形的面积即可;
相应线段的长,再从矩形中减去旁边三个三角形的面积即可;
(2)先求出△BPQ的面积的函数关系式,根据函数性质即可得到结果;
分0≤ t ≤ 2、2< t ≤ 4、4< t < 8三种情况讨论。
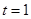 相应线段的长,再从矩形中减去旁边三个三角形的面积即可;
相应线段的长,再从矩形中减去旁边三个三角形的面积即可;(2)先求出△BPQ的面积的函数关系式,根据函数性质即可得到结果;
分0≤ t ≤ 2、2< t ≤ 4、4< t < 8三种情况讨论。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
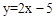 与x轴和y轴分别交于点A和点B,抛物线
与x轴和y轴分别交于点A和点B,抛物线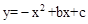 的顶点M在直线AB上,且抛物线与直线AB的另一个交点为N.
的顶点M在直线AB上,且抛物线与直线AB的另一个交点为N.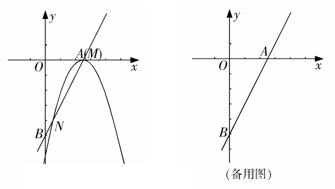
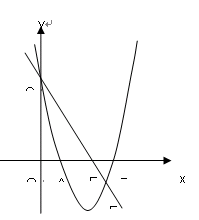
 (
( )的图象如图所示,有下列结论:①
)的图象如图所示,有下列结论:① ;②
;② ;③
;③ ;④
;④ .其中,正确结论的个数是
.其中,正确结论的个数是
 (单位:分钟)与学习收益量
(单位:分钟)与学习收益量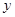 的关系如图1所示,用于回顾反思的时间
的关系如图1所示,用于回顾反思的时间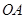 是抛物线的一部分,
是抛物线的一部分,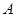 为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
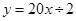

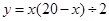
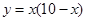
 ,对角线AC与BD相交于O,AB=8cm,AD=10cm,BC=6cm,一个动点E从点B出发,以每秒1cm的速度沿射线BA方向移动,过E作EQ⊥AB,交直线AC于P,交直线BD于Q,以PQ为边向上作正方形PQMN,设正方形PQMN与△BOC,重叠部分的面积为s,点E的运动时间为t秒.
,对角线AC与BD相交于O,AB=8cm,AD=10cm,BC=6cm,一个动点E从点B出发,以每秒1cm的速度沿射线BA方向移动,过E作EQ⊥AB,交直线AC于P,交直线BD于Q,以PQ为边向上作正方形PQMN,设正方形PQMN与△BOC,重叠部分的面积为s,点E的运动时间为t秒.
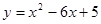 的部分图象如图,则抛物线的对称轴为直线x= ,满足y<0的x的取值范围是 ,将抛物线
的部分图象如图,则抛物线的对称轴为直线x= ,满足y<0的x的取值范围是 ,将抛物线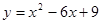 .
.
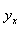 表示与自变量
表示与自变量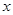 所对应的函数值。例如对于函数
所对应的函数值。例如对于函数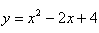 ,当
,当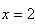 时,对应的函数值
时,对应的函数值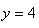 ,则可以写为:
,则可以写为: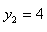 。在二次函数
。在二次函数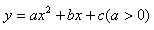 中,若
中,若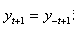 对任意实数
对任意实数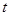 都成立,那么下列结论错误的是( )
都成立,那么下列结论错误的是( )