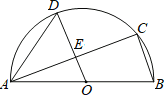
题目内容
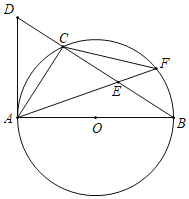
【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=10,AC=8,求DE的长.
【答案】(1)35°;(2)2
【解析】
(1)由AB是半圆O的直径,根据直径所对的圆周角是直角,可得∠C=90°,又由OD∥BC,可求得∠AEO的度数,然后求得∠CAB的度数,继而求得答案;
(2)由勾股定理,首先求得BC的长,然后由三角形中位线的性质,求得OE的长,继而求得答案.
(1)∵AB是半圆O的直径,
∴∠ACB=90°,
又∵OD∥BC,
∴∠AEO=90°,
即OE⊥AC,∠CAB=90°﹣∠B=90°﹣70°=20°.
∵OA=OD,
∴∠DAO=∠ADO=![]() (180﹣70)°=55°,
(180﹣70)°=55°,
∴∠CAD=∠DAO﹣∠CAB=55°﹣20°=35°;
(2)在直角△ABC中,BC=![]() =6.
=6.
∵OE⊥AC,
∴AE=EC=4,
又∵OA=OB,
∴OE=![]() BC=3,
BC=3,
又∵OD=![]() AB=5,
AB=5,
∴DE=OD-OE=5-![]() =2.
=2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法正确的个数是( )
①抛物线与x轴的一个交点为(﹣2,0);
②抛物线与y轴的交点为(0,6);
③抛物线的对称轴是x=1;
④在对称轴左侧y随x增大而减小;
⑤当y>0,则x的取值范围是-2<x<3
A.①②③B.②③④C.②④⑤D.①②⑤