题目内容
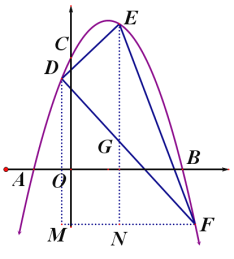
【题目】如图,已知二次函数 ![]() 的图象经过点C(0,3),与
的图象经过点C(0,3),与![]() 轴分别交于点A、点B(3,0).点
轴分别交于点A、点B(3,0).点![]() 、
、![]() 、
、![]() 都在这个二次函数的图象上,其中0<
都在这个二次函数的图象上,其中0<![]() <4,连接DE、DF、EF,记△DEF的面积为S.
<4,连接DE、DF、EF,记△DEF的面积为S.
(1)求二次函数![]() 的表达式;
的表达式;
(2)若![]() =0,求S的最大值,并求此时
=0,求S的最大值,并求此时![]() 的值;
的值;
(3)若![]() =2,当
=2,当![]() 取不同数值时,S的值是否变化,如不变,求该定值;如变化,试用含
取不同数值时,S的值是否变化,如不变,求该定值;如变化,试用含![]() 的代数式表示S.
的代数式表示S.
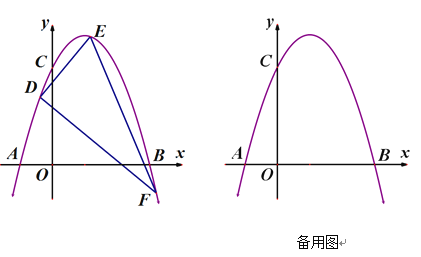
【答案】(1)y=﹣x2+2x+3;(2)当t=2时,S的最大值为8;(3)当![]() 取不同数值时,S的值永远为8,理由见解析
取不同数值时,S的值永远为8,理由见解析
【解析】
(1)将点B和点C的坐标代入函数解析式,用待定系数法即可求出函数解析式;
(2)先求出直线DF的解析式,设点G的坐标为(t,﹣2t+3),用含t的代数式表示出EG的长,进而可列出S关于t的关系式,再根据二次函数的性质求出结论;
(3)用含n的代数式表示出DM、EN的长,然后根据,S=![]() 解答即可.
解答即可.
解:(1)将点B和点C的坐标代入函数解析式,得
![]() ,解得
,解得![]() ,
,
二次函数的解析是为y=﹣x2+2x+3;
(2)E在抛物线上,E(t,﹣t2+2t+3),
设直线DF的解析式为y=kx+b,
将点D和点F的坐标代入函数解析式,求得直线DF的解析式为y=﹣2x+3,
设点G的坐标为(t,﹣2t+3),
EG=﹣t2+2t+3﹣(﹣2t+3)=﹣t2+4t.
S=![]() EG×4=﹣2t2+8t=-2(t-2)2+8,
EG×4=﹣2t2+8t=-2(t-2)2+8,
当t=2时,S的最大值为8,
此时t=2.
(3)当![]() 取不同数值时,S的值不变,
取不同数值时,S的值不变,
∵点![]() 、
、![]() 、
、![]() 都在这个二次函数的图象上,
都在这个二次函数的图象上,
∴![]() 、
、![]() 、
、![]()
DM=8n+8,EN=4n+8,S=![]() =(12n+16)+(4n+8)-2(8n+8)=8.
=(12n+16)+(4n+8)-2(8n+8)=8.
所以,当![]() 取不同数值时,S的值永远为8.
取不同数值时,S的值永远为8.

练习册系列答案
相关题目