题目内容
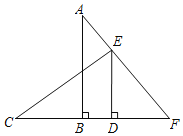
【题目】如图，在四边形ABCD中，点E为CD的中点，连接AE延长交BC的延长线于点F，连接BE，AE＝FE，BE⊥AF．
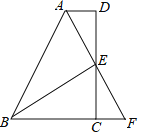
（1）求证：△AED≌△FEC
（2）求证：AB＝BC＋AD
【答案】（1）见解析；（2）见解析
【解析】
（1）先利用中点证明DE=CE，再用SAS证明△AED≌△FEC即可；
（2）由AE=FE， BE⊥AF可知BE垂直平分AF，则有AB=FB，利用全等可得出AD=FC，则结论可证．
证明：（1）∵点E为CD的中点
∴DE=CE
在△AED与△FEC中，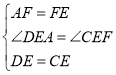
∴△AED≌△FEC（SAS）
（2）∵AE=FE， BE⊥AF
∴BE垂直平分AF
∴AB=FB
由（1）得：△AED≌△FEC
∴AD=FC
∴AB=FB =BC+FC =BC+AD
练习册系列答案
一线名师权威作业本系列答案
相关题目
【题目】为了争创全国文明卫生城市，优化城市环境，节约能源，某市公交公司决定购买一批共10台全新的混合动力公交车，现有A、B两种型号，其中每台的价格，年省油量如下表：
A | B | |
价格（万元／台） | a | b |
节省的油量（万升／年） | 2.4 | 2 |
经调查，购买一台A型车比购买一台B型车多10万元，购买3台A型车比购买4台B型车少30万元．
（1）请求出a和b的值；
（2）若购买这批混合动力公交车（两种车型都要有）每年能节省的油量不低于21.6万升，请问有几种购车方案？请写出解答过程．
（3）求（2）中最省钱的购车方案及所需的购车款．
