题目内容
【题目】东方公园的门票价格如下表所示:
购票人数 | 1~50人 | 51~100人 | 100人以上 |
每人门票价 | 13元 | 11元 | 9元 |
某校初一(1)(2)两个班去游览东方公园,其中(1)班人数较少,不足50人;(2)班人数较多,有50多人,但两个班合起来超过100人. 如果两个班都以班为单位分别购票,则一共应付1240元;如果两个班联合起来,作为一个团体购票,则只需付936元.
(1)列方程或方程组求出两个班各有多少学生?
(2)如果两个班不联合买票,是不是初一(1)班的学生非要买13元的票呢?你有什么省钱方式来帮他们买票呢?说说你的理由.
(3)你认为是否存在这样的可能:51~100人之间买票的钱数与100人以上买票的钱数相等?如果有,是多少人与多少人买票钱数相等?
【答案】(1)初一(1)班有学生48人,(2)班有学生56人;(2)初一(1)班的学生不一定非要买13元的票,48人买51人的票可以更省钱,理由见解析;(3)存在,90人与110人,99人与121人.
【解析】
(1)设初一(1)、(2)两个班各有学生x、y人,根据题意列方程组即可求解;
(2)求出初一(1)班的学生买13元的票和买51人的票的钱数比较即可解答;
(3)假设存在买票钱数相等的状况,即:人数在51~100人之间时的人数×相应的票价=人数在100人以上时的人数×相应的票价,如果有满足等量关系的量,则成立,反之,则不成立.
解:(1)设初一(1)、(2)两个班各有学生x、y人,
则由题意得: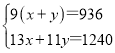 ,
,
解得:![]() ,
,
答:初一(1)班有学生48人,(2)班有学生56人;
(2)初一(1)班的学生不一定非要买13元的票.
理由如下:由(1)可知初一(1)班48人,只需多买3张,
51×11=561,48×13=624>561,
∴48人买51人的票可以更省钱.
(3)设51~100人之间有m人,100人以上有n人.
假设存在买票钱数相等的状况.
就是满足11m=9n,
∵m<100,n>100,
∴符合题意的正整数解,各为90人与110人,99人与121人.

【题目】九年级甲、乙两名同学期末考试的成绩(单位:分)如下:
语文 | 数学 | 英语 | 历史 | 理化 | 体育 | |
甲 | 75 | 93 | 85 | 84 | 95 | 90 |
乙 | 85 | 85 | 91 | 85 | 89 | 85 |
根据表格中的数据,回答下列问题:
(1)甲的总分为522分,则甲的平均成绩是__________分,乙的总分为520分,________的成绩好一些. (填“甲”或者“乙”)
(2)经过计算知![]() . 你认为__________不偏科;(填“甲”或者“乙”)
. 你认为__________不偏科;(填“甲”或者“乙”)
(3)中招录取时,历史和体育科目的权重是0.3,其它科成绩权重是1,请问谁的成绩更好一些?请说明理由.
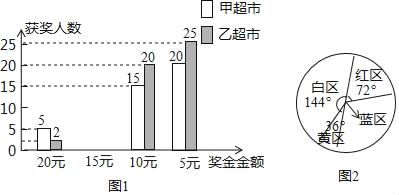
【题目】两家超市同时采取通过摇奖返现金搞促销活动,凡在超市购物满100元的顾客均可以参加摇奖一次.小明和小华对两家超市摇奖的50名顾客获奖情况进行了统计并制成了图表(如图)
奖金金额 获奖人数 | 20元 | 15元 | 10元 | 5元 |
商家甲超市 | 5 | 10 | 15 | 20 |
乙超市 | 2 | 3 | 20 | 25 |
(1)在甲超市摇奖的顾客获得奖金金额的中位数是 ,在乙超市摇奖的顾客获得奖金金额的众数是 ;
(2)请你补全统计图1;
(3)请你分别求出在甲、乙两超市参加摇奖的50名顾客平均获奖多少元?
(4)图2是甲超市的摇奖转盘,黄区20元、红区15元、蓝区10元、白区5元,如果你购物消费了100元后,参加一次摇奖,那么你获得奖金10元的概率是多少?
【题目】某新建小区要修一条1050米长的路,甲、乙两个工程队想承建这项工程.经
了解得到以下信息(如表):
工程队 | 每天修路的长度(米) | 单独完成所需天数(天) | 每天所需费用(元) |
甲队 | 30 | n | 600 |
乙队 | m | n﹣14 | 1160 |
(1)甲队单独完成这项工程所需天数n= ,乙队每天修路的长度m= (米);
(2)甲队先修了x米之后,甲、乙两队一起修路,又用了y天完成这项工程(其中x,y为正整数).
①当x=90时,求出乙队修路的天数;
②求y与x之间的函数关系式(不用写出x的取值范围);
③若总费用不超过22800元,求甲队至少先修了多少米.