Question

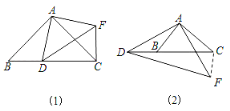
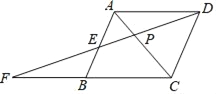
【题目】如图，在菱形ABCD中，P是对角线AC上的一点，连结DP并延长交AB于点E，交CB的延长线于点F．若DP=3，EF=，则PE的长是（　　）

A. B. C. 2 D.

Answer 1

【答案】B

【解析】

连接BP，根据菱形的性质证明△ABP≌△APD，即可得∠ABP=∠ADP，结合平行线的性质可证得∠F=∠ADP=∠ABP，再证明△EBP∽△FBP，根据相似三角形的性质可得PB2=PEPF．因BP=PD，DP=3，EF=2，由此即可求得PE的长.

连接BP，

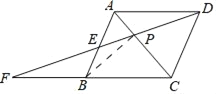
∵四边形ABCD是菱形，

∴AB=AD，∠BAP=∠DAP．

又∵AP=AP，

∴△ABP≌△APD，

∴∠ABP=∠ADP，

∵AD∥BC，

∴∠F=∠ADP=∠ABP，

又∵∠BPE=∠BPF，

∴△EBP∽△BFP．

∴ ．

∴PB2=PEPF．

∵△ABP≌△ADP，

∴BP=PD．

∴PD2=PEPF，

∵DP=3，EF=2，

∴PE=，

故选B．