题目内容
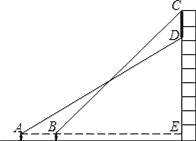
【题目】如图所示，小杨在广场上的A处正面观测一座楼房墙上的广告屏幕，测得屏幕下端D处的仰角为30°，然后他正对大楼方向前进5m到达B处，又测得该屏幕上端C处的仰角为45°．若该楼高为26.65m，小杨的眼睛离地面1.65m，广告屏幕的上端与楼房的顶端平齐．求广告屏幕上端与下端之间的距离．（
≈1.732，结果精确到0.1m）
【答案】7.7
【解析】试题分析：易得CE=BE，利用30°的正切值即可求得CE长，进而可求得DE长．CE减去DE长即为广告屏幕上端与下端之间的距离．
试题解析：设AB、CD的延长线相交于点E．
∵∠CBE=45°，CE⊥AE，
∴CE=BE．
∵CE=26.65﹣1.65=25，
∴BE=25．
∴AE=AB+BE=30．
在Rt△ADE中，∠DAE=30°，
∴DE=AE×tan30°=30×
=10
，
∴CD=CE﹣DE=25﹣10≈25﹣10×1.732=7.68≈7.7（m）．
答：广告屏幕上端与下端之间的距离约为7.7m．
练习册系列答案
口算能手系列答案
相关题目
