题目内容
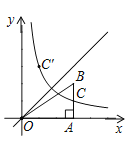
【题目】如图，在平面直角坐标系中，点B在第一象限，BA⊥x轴于点A，反比例函数y＝
（x＞0）的图象与线段AB相交于点C，C是线段AB的中点，点C关于直线y＝x的对称点C'的坐标为（m，6）（m≠6），若△OAB的面积为12，则k的值为（ ）
A.4B.6C.8D.12
【答案】D
【解析】
根据对称性求出C点坐标，进而得OA与AB的长度，再根据已知三角形的面积列出m的方程求得m，进而用待定系数法求得k．
解：∵点C关于直线y＝x的对称点C'的坐标为（m，6）（m≠6），
∴C（6，m），
∴OA＝6，AC＝m，
∴AB＝2AC＝2m，
∵三角形OAB的面积为12，
∴
＝12，
解得，m＝2，
∴C（6，2），
∴k＝6×2＝12．
故选：D．
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
